Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 124
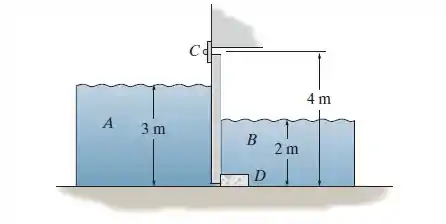
Quando a água da maré diminui, a comporta automaticamente se abre para drenar o pântano . Para a condição de maré alta mostrada, determine as reações horizontais desenvolvidas na dobradiça e no bloco de detenção . O comprimento da comporta é de 6 m e sua altura é de 4 m. .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
O objetivo desta questão é descobrirmos as forças que atuam tanto em quanto em (ambas horizontais).
Para isso, nós temos que analisar a comporta na vertical. Portanto, as forças hidrostáticas possuem apenas uma componente horizontal, aplicadas em algum ponto da barra (que iremos descobrir).
O primeiro passo para resolvermos esta questão é determinar as forças resultantes devido à pressão hidrostática. Só depois vamos ter informações para calcular as forças em e em .
Então, vamos as contas!
Passo 2
Vamos começar determinando a força resultante e aonde ela atua pelo lado . Esta força será exatamente:
Sendo e a intensidade da carga medida nos pontos superior e inferior do nível da água (pelo lado ). Para obtermos os seus valores, basta multiplicar a espessura da comporta pela pressão em cada um dos pontos. Logo,
Então,
Já o ponto de atuação desta força, medido a partir da superfície do líquido (com o ar), é:
Mas isto medido a partir da superfície viu! Se formos medir a partir do ponto , ele será:
Passo 3
Agora temos que analisar a força para o lado .
Para este caso, temos:
Então,
Já o ponto de atuação desta força, medido a partir da superfície do líquido (com o ar), é:
Mas isto medido a partir da superfície viu! Se formos medir a partir do ponto , ele será:
Passo 4
Agora vamos para a barra . Aqui é a boa e velha questão de equilíbrio estático.
Temos uma barra em equilíbrio com cinco forças, as hidrostáticas e , as forças no pino , e , e as forças em , .
Então, basta utilizarmos as equações de equilíbrio. Portanto,
Resolvendo o sistema acima nós obtemos:
E assim finalizamos a questão!