Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 144

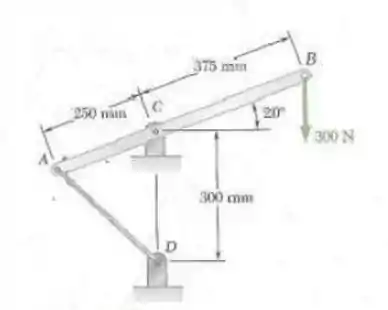
Uma alavanca AB é articulada em C e presa a um cabo de controle em A. Se a alavanca for submetida a uma força vertical de 300 N em B, determine (a) a tração no cabo, (b) a reação em C

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Precisamos determinar a tração no cabo AD ( T ) e a reção em C. T é na direção do cabo (ângulo α ). Para a reação em C encontraremos as componentes C X   e   C Y .

Olhando para a imagem do enunciado, podemos notar que todas as forças estão em N (Newtons) e todas as medidas em mm (milímetros). Portanto não precisaremos fazer conversçoes.

Passo 2

Primeiramente consideraremos o triângulo ACD, representado abaixo, para determinar o ângulo α = C Â D : Aplicaremos a regra dos cossenos duas vezes, a primeira para encontra o seguimento AD, uma vez que o ângulo oposto a ele é conhecido (90°-20°), e depois aplicaremos para encontrar o ângulo 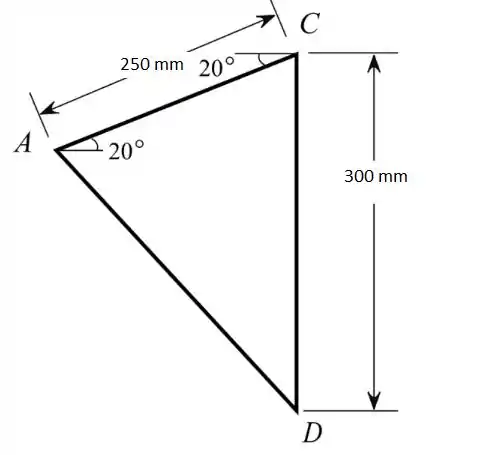α .

A D 2 = A C 2 + C D 2 - 2 ∙ A C ∙ C D ∙ cos ⁡ ( 90 ° - 20 ° )

A D = A C 2 + C D 2 - 2 ∙ A C ∙ C D ∙ cos ⁡ 90 ° - 20 °

A D = 250 2 + 300 2 - 2 ∙ 250 ∙ 300 ∙ cos ⁡ ( 90 ° - 20 ° )

A D = 318,11   m m

Aplicando novamente para encontrar o seguimento CD:

C D 2 = A C 2 + A D 2 - 2 ∙ A C ∙ A D ∙ cos ⁡ ( α )

α = A C 2 + A D 2 - C D 2 2 ∙ A C ∙ C D

α = 60,6 °

Passo 3

Analisaremos agora o diagrama de corpo livre abaixo.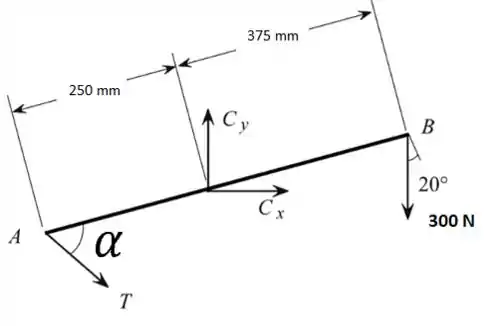

Podemos aplicar o somatório dos momentos em torno de C para determinar a tração T

↺ + ∑ M C =0

T ∙ s e n   α ∙ 250 - 300 ∙ cos ⁡ 20 ° ∙ 375 = 0

T = 485,37   N

T indica a tração no cabo AD.

Passo 4

Nesse passo encontraremos a reação em C

Podemos aplicar o somatório das forças horizontais → + ∑ F x para encontrar a componente C X :

→ + ∑ F x

T ∙ cos ⁡ α - 20 ° + C X = 0

485,37 ∙ cos ⁡ 40,6 ° + C X = 0

C X = - 368,52   N

] C X = 368,52   N ←

C x indica a reação horizontal no ponto X. Observe que o sinal foi negativo, o que indica que a direção da resultante é a mesma do diagrama de corpo livre, da esquerda para a direita.

Faremos agora o somatório de forças em verticais, temos que:

↑ + ∑ F y

T ∙ sen ⁡ α - 20 ° + C Y - 300 = 0

C Y = 615,87   N ↑

C y indica a componente vertical da reação em C. Observe que o sinal foi positivo, o que indica que a direção da resultante é a mesma do diagrama, de baixo pra cima.

Finalmente podemos encontrar o valor de C e sua direção:

R C = C X 2 + C Y 2 = 600 2 + ( - 615,87 ) 2

R C = 640,8

θ = t g - 1 R C Y R C X = t g - 1 615,88 368,52

θ = 20,56 °     c o m   o   e i x o   x   n o   s e g u n d o   q u a d r a n t e

Resposta

  1. Tração no cabo

    2. T = 485,37   N

  2. Reação em C

R C = 640,8

θ = 20,56 °     c o m   o   e i x o   x   n o   s e g u n d o   q u a d r a n t e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe o diagrama de corpo livre para os problemas a seguir.O elemento em " L " no Problema 5 . 25 .O guindaste e a lança no Problema 5 . 26 .O elemento no Problema 5 . 27 .A haste no Problema 5 . 28
Desenhe o diagrama de corpo livre para os problemas a seguir.A viga no Problema 5 . 52 .O menino e o trampolim no Problema 5 . 53 .O conjunto da plataforma no Problema 5 . 54 .A haste no Problema 5 .
Desenhe o diagrama de corpo livre para os problemas a seguir.A viga no Problema 5 . 32 .O guindaste no Problema 5 . 33 .A lança A B no Problema 5 . 35 .O tubo liso no Problema 5 . 36 .
Desenhe o diagrama de corpo livre para os problemas a seguir.A haste no Problema 5 . 44 .O carrinho de mão e a carga quando levantados no Problema 5 . 45 .A viga no Problema 5 . 47 .O dispositivo no P
Determine as reações nos apoios.