Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 143

Determine as reações em A e C quando (a) α = 0 , (b) α = 0

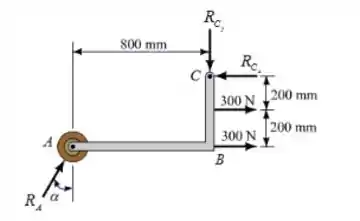
Figura P4.143

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Precisamos determinar as reações em A e C para duas condições diferentes: quando α = 0 e α = 30 ° .

Olhando para a imagem do enunciado, podemos notar que todas as forças estão em N (Newtons) e todas as medidas estão em mm (milímetros). Portanto, não precisaremos converter unidades e as reações serão encontradas em N .

O apoio do rolete em A produz apenas reação perpendicular ao solo, já o apoio em C produz reações C x   e   C y .

Passo 2

Agora consideraremos o seguinte diagrama de corpo livre:

Passo 3

Primeiramente encontraremos as relações em função de α :

Consideraremos o somatório dos momentos em torno de C ( ∑ M C ) para encontrar a reação R A :

↺ + ∑ M C =0

- R A ∙ cos ⁡ α . ∙ 800 + - R A ∙ sen ⁡ α . ∙ 200 + 200 + 300 ∙ 200 + 200 + 300 ∙ 200 = 0

- R A ∙ cos ⁡ α . ∙ 800 + - R A ∙ sen ⁡ α . ∙ 400 + 180000 = 0

Uma vez resolvida para um determinado valor de α e encontrado o valor correspondente de R A , poderemos aplicar o somatório das forças na vertical e na horizontal ( ∑ F y   e   ∑ F x ,   respectivamente) para encontrar as reações R C Y e R C X :

↑ + ∑ F y = 0

R A ∙ cos ⁡ α . ∙ - R C Y = 0

↑ + ∑ F x = 0

300 + 300 + R A ∙ sen ⁡ α . - R C X = 0

600 + R A ∙ sen ⁡ α . - R C X = 0

Passo 4

Substituiremos agora o valor de α =0° nas relações obtidas no passo 2, resolvendo assim o item (a):

- R A ∙ cos ⁡ 0 . ∙ 800 + - R A ∙ sen ⁡ 0 . ∙ 400 + 180000 = 0

R A = 225   N

R A indica a reação no rolete para o ângulo α =0°

Agora substituiremos R A na relação das forças verticais para determinar C Y

225 ∙ cos ⁡ α . ∙ - R C Y = 0

R C Y = 225   N ↓

R C Y indica a reação vertical no ponto C, o sinal positivo mostra que o sentido é o mesmo arbitrado no diagrama de corpo livre, ou seja, para baixo.

Aplicando na relação para as forças horizontais teremos:

600 + 225 ∙ sen ⁡ 0 . - R C X = 0

R C X = 60 0 N   ←

R C Y indica a reação horizontal no ponto C, o sinal positivo mostra que o sentido é o mesmo arbitrado no diagrama de corpo livre, ou seja, da direita para a esquerda.

Finalmente a reação R C e sua orientação θ   podem ser encontradas :

R C = R C X 2 + R C Y 2 = 600 2 + 225 2

R C = 640,8

θ = t g - 1 R C Y R C X = t g - 1 225 600

θ = 20,56 °   n o   t e r c e i r o   q u a d r a n t e

Passo 5

Repetiremos agora o passo 4 com o valor de α =30°, resolvendo assim o item (a):

- R A ∙ cos ⁡ 30 ° . ∙ 800 + - R A ∙ sen ⁡ 30 ° . ∙ 400 + 180000 = 0

R A = 365,24   N

R A indica a reação no rolete para o ângulo α =30°

Agora substituiremos R A na relação das forças verticais para determinar C Y

365,24 ∙ cos ⁡ 30 ° . ∙ - R C Y = 0

R C Y = 316,3   N ↓

R C Y indica a reação vertical no ponto C, o sinal positivo mostra que o sentido é o mesmo arbitrado no diagrama de corpo livre, ou seja, para baixo.

Aplicando na relação para as forças horizontais teremos:

600 + 365,24 ∙ sen ⁡ 30 ° . - R C X = 0

R C X = 782,62 N   ←

R C Y indica a reação horizontal no ponto C, o sinal positivo mostra que o sentido é o mesmo arbitrado no diagrama de corpo livre, ou seja, da direita para a esquerda.

Finalmente a reação R C e sua orientação θ   podem ser encontradas :

R C = R C X 2 + R C Y 2 = 782,62 2 + 316,3 2

R C = 844,12   N

θ = t g - 1 R C Y R C X = t g - 1 316,3 782,62

θ = 22 °   n o   t e r c e i r o   q u a d r a n t e

Resposta

  1. Para α =0 :

    2. R A = 225   N

    R C = 640,8 com orientação θ = 20,56 °   n o   t e r c e i r o   q u a d r a n t e

  2. Para α =30°:

R A = 365,24   N

R C = 844,12   N com orientação θ = 22 °   n o   t e r c e i r o   q u a d r a n t e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As molas BA e BC possuem uma rigidez de 500 N/m cada e um comprimento não esticado de 3 m. Determine a força horizontal F aplicada à corda que está presa ao pequeno anel B, de modo que o deslocamento
Determine a tração desenvolvida em cada um dos fios usados para o equilíbrio da luminária de 20 kg.
A caixa tem um peso de 550N . Determine a força em cada cabo de sustentação.
O tubo é mantido no lugar pela morsa. Se o parafuso exerce uma força de 300N sobre o tubo na direção indicada, determine as intensidades F A e F B das forças que os contatos lisos em A e B exercem sob
Determine o máximo de massa do motor que pode ser suportada sem exceder uma tração de 2k N na corrente AB e 2,2k N na corrente AC.