Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 67

Para ambas as condições (a) e (b), conforme declarado no Prob. 6/66, determine a magnitude e a direção da força P necessária para começar a abaixar o corpo de 100 lb.

Passo 1

Primeiro, vamos desenhar o diagrama de corpo livre do corpo de 100 lb

Sabemos que o coeficiente de atrito estático entre o corpo e a cunha é μA = 0,20, portanto podemos calcular o ângulo ϕA

ϕ A = t a n - 1 ⁡ ( 0.20 ) ϕ A = 11.31 ∘

Equacionando a soma das forças na direção y a zero, podemos determinar a força de reação RA

∑ F y = 0

- 100 + R A c o s ⁡ 15 ∘ - ϕ A = 0 R A = 100 cos ⁡ 15 ∘ - ϕ A R A = 100 cos ⁡ 15 ∘ - 11.31 ∘ R A = 100.21 l b

Passo 2

Desenharemos o diagrama de corpo livre da cunha

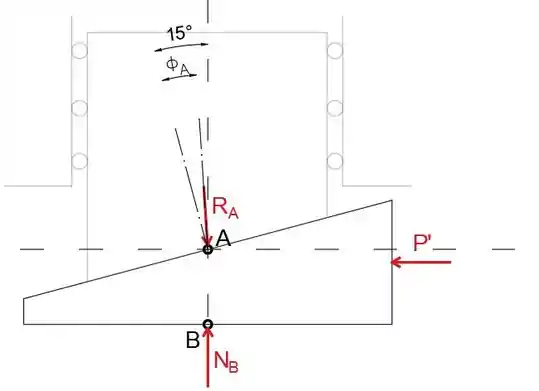
Equacionando a soma das forças na direção x a zero, podemos determinar a força P necessária para elevar o corpo

∑ F x = 0

R A s i n ⁡ 15 ∘ - ϕ A - P ' = 0 P ' = R A s i n ⁡ 15 ∘ - ϕ A P ' = 100.21 s i n ⁡ 15 ∘ - 11.31 ∘ P ' = 6.45 l b   p a r a   a   e s q u e r d a  

Passo 3

(b) Novamente, vamos desenhar o diagrama de corpo livre da cunha, mas observe que há atrito no ponto B agora

Sabemos que o coeficiente de atrito estático entre o solo e a cunha é μB = 0,20, portanto, podemos calcular o ângulo ϕB

ϕ B = t a n - 1 ⁡ ( 0.20 ) ϕ B = 11.31 ∘

Equacionando a soma das forças na direção y a zero, podemos determinar a força de reação RC

∑ F y = 0

- R A c o s ⁡ 15 ∘ - ϕ A + R C c o s ⁡ ϕ B = 0 - 100.21 c o s ⁡ 15 ∘ - 11.31 ∘ + R C c o s ⁡ 11.31 ∘ = 0 R C = 100.21 c o s ⁡ 3.69 ∘ cos ⁡ 11.31 ∘ R C = 101.98 l b

Equacionando a soma das forças na direção x a zero, podemos determinar a força P necessária para elevar o corpo

∑ F x = 0

R A s i n ⁡ 15 ∘ - ϕ A - R C s i n ⁡ ϕ B + P ' = 0 P ' = - R A s i n ⁡ 15 ∘ - ϕ A + R C s i n ⁡ ϕ B P ' = - 100.21 s i n ⁡ 15 ∘ - 11.31 ∘ + 101.98 s i n ⁡ 11.31 ∘ P ' = 13.55 l b   p a r a   a   d i r e i t a

Resposta

( a ) P ' = 6.45  lb para a esquerda

(b) P ' = 13.55 l b  para a direita

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
Na morsa de bancada mostrada, o mordente móvel D está rigidamente ligado a lingueta A B que se encaixa com folga no corpo fixo da morsa. O parafuso de rosca simples é rosqueado na base fixa e tem um d
Considerando no Problema 8.70 que uma rosca à direita seja usada em ambas as barras A e B , determine a intensidade do torque que deve ser aplicado à luva a fim de girá-la.
No problema 8.72 , a força de aperto de 4,5N foi obtida apertando-se a morsa. Determine o torque que deve ser aplicado ao parafuso para afrouxar a morsa.