As extremidades da braçadeira de tubo são projetadas para caber em 1/2 pol. Padrão. tubo de água de aço (diâmetro externo = 0,840 pol.). A conexão direita desliza livremente ao longo do tubo quando a alavanca C é levantada para liberar seu contato com o tubo, como pode ser visto na visão expandida. Sob uma carga de aperto F, o encaixe direito entra em contato com o tubo em A e B apenas, pois seu encaixe frouxo permite que ele gire ligeiramente no sentido horário no tubo. Determine (a) os coeficientes mínimos de atrito estático μs entre as superfícies de contato em A e B de modo que o encaixe final não deslize sob a carga e
(b) a força R suportada pelo pino em O sob uma força de aperto F = 800 lb. A força da mola sob a projeção da alavanca é desprezível.
Passo 1
(a) Primeiro, vamos isolar a alavanca C Observe que a mola não está esticada, portanto, ela exerce força zero na alavanca
A fim de encontrar o coeficiente mínimo de atrito (μn) A, devemos assumir que FA é a força máxima de atrito
(1)

Passo 2
Equacionando a soma dos momentos sobre o ponto O a zero, determinaremos o coeficiente mínimo de atrito (μs) A
Substitua F1 na equação (1)
Em seguida, vamos isolar a conexão direita sem o tubo
Observe que devemos assumir que o deslizamento ocorre simultaneamente em A e B para que o problema seja resolvido
Isso significa que FB também é a força de atrito máxima
(2)
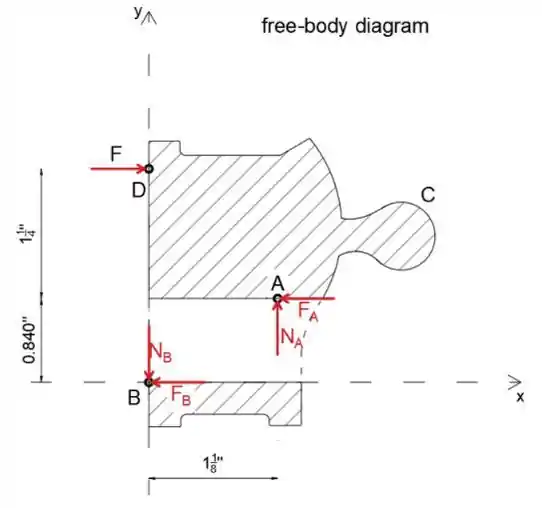
Passo 3
Equacionando a soma da força na direção y sobre o ponto O a zero, determinaremos a força de reação normal em A e B
Substituiremos NA e NB na equação (2)
(3)
Equacionando a soma dos momentos sobre o ponto D a zero, determinaremos o coeficiente mínimo de atrito (μs)B
Substituiremos FA e FB pelas expressões (1) e (3)
Substituiremos por seu valor
Passo 4
(b) Novamente, vamos isolar a conexão direita sem o tubo
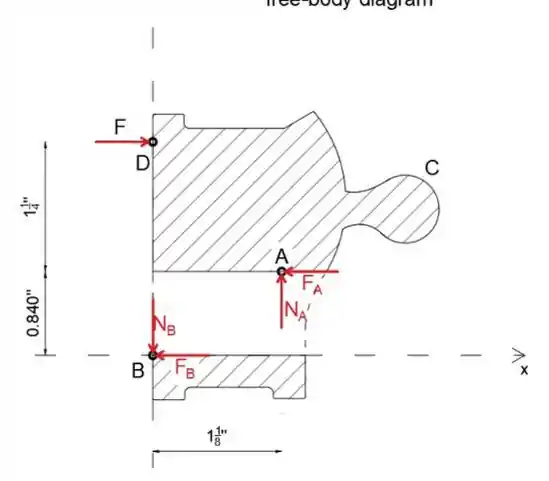
Ao igualar a soma da força na direção x a zero, obteremos uma equação com apenas uma incógnita
Em seguida, calcularemos a força de atrito FA, pois sabemos que o coeficiente de atrito (μs) A = 0,25
Passo 5
Finalmente, vamos isolar a alavanca C
Ao igualar a soma das forças na direção x - e y - a zero, podemos determinar OX e OY
Usando o teorema de Pitágoras, determinaremos a magnitude da força resultante em O
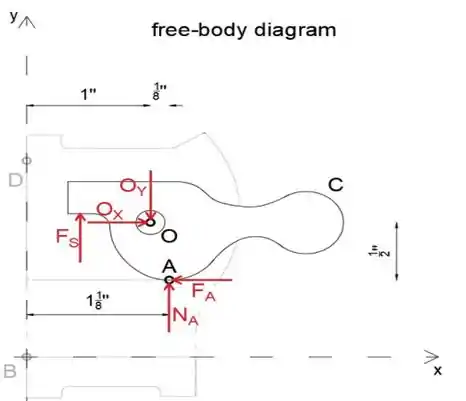
Resposta
(b)