Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 109

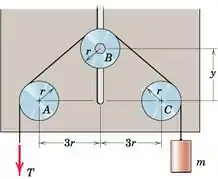
As posições dos eixos A e C são fixas, enquanto que as do eixo B podem ser variadas por meio da fenda vertical e do parafuso de travamento. Se o coeficiente de atrito estático for m em todas as interfaces, determine a dependência de T na coordenada y, onde T é a tensão necessária para começar a levantar o cilindro de massa m. Todos os eixos são fixos contra rotação.

Passo 1

Como estamos tentando levantar o cilindro, sabemos que a tensão T é maior que o peso W, sabendo que o coeficiente de atrito é igual para todas as superfícies, podemos escrever a expressão para a tensão T como

T = W ∙ e μ β

T = m g ∙ e μ β

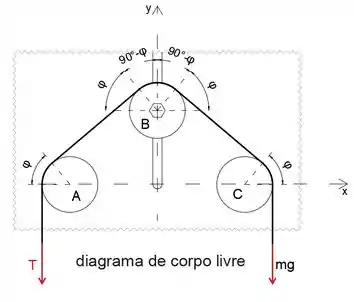
Passo 2

O ângulo de contato β é igual à soma dos ângulos de contato em cada eixo, olhando para o esboço acima, podemos escrever isso como

β = φ + 90 ° - φ + 90 ° - φ + φ

β = 180 °

β = π   rad

Vamos substituir β por seu valor na expressão (1) para obter a expressão final para a tensão T

T = m g ∙ e μ β                     ( 1 )

T = m g ∙ e μ π

Resposta

T = m g ∙ e μ π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A extremidade A de uma haste delgada e uniforme de comprimento L e peso W é mantida em equilíbrio na superfície como mostrado na figura, enquanto a extremidade B é suportada por uma corda BC. Sabendo
Uma janela corrediça pesando 50 N é geralmente sustentada por dois pesos de 25 N. Sabendo que a janela permanece aberta depois que uma das cordas dos pesos foi cortada, determine o menor valor possíve
Uma escada AB de 6,5 m encosta-se em uma parede como mostrado na figura. Considerando que o coeficiente de atrito estático μ s é zero em B, determine o menor valor de μ s em A para que o equilíbrio se
A extremidade A de uma haste delgada e uniforme de comprimento L e peso W é mantida em equilíbrio na superfície como mostrado na figura, enquanto a extremidade B é suportada por uma corda BC. Sabendo
Um bloco de concreto de 500 N é elevado por um par de pinças mostrado na figura. Determine o menor valor admissível do coeficiente de atrito estático entre o bloco e as pinças em F e G.