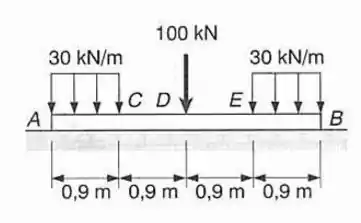
Assumindo que a reação do solo sobre a viga, de baixo para cima, se distribui uniformemente, desenhar os diagramas de força cortante e de momento fletor para a viga com carregamento mostrado e determinar o máximo valor absoluto: (a) da força cortante; (b) do momento fletor.

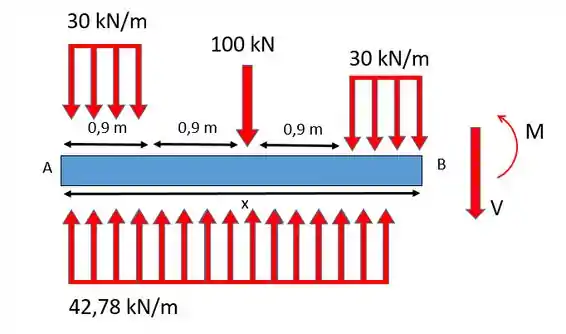
Aqui temos um caso em que a barra está apoiada no solo e o problema nos diz que a força resultante será igualmente distribuída pela barra, ou seja, vamos ter algo assim:

Observe que colocamos uma força distribuída como a reação do solo. Para calcular essa força a gente vai fazer o somatório das forças em igual a zero:

Como a barra está dividida em 4 partes iguais de 0,9 metros vamos ter que cada força distribuída de vai valer:

Colocando na nossa equação:

Logo a força de reação do solo vale:

Mas essa é uma força distribuída então a gente precisa distribui-la por toda a extensão da barra, que é de assim:

Show de bola calculamos a reação na barra!

Agora vamos realizar as seções e, como dito anteriormente, essas seções ocorrem em lugares específicos, basicamente sempre que houver mudança no carregamento de carga.

Neste caso vamos fazer 4 seções: Entre AC, entre CD, entre DE e entre EB. Vamos olhar cada seção.

Seção AC:

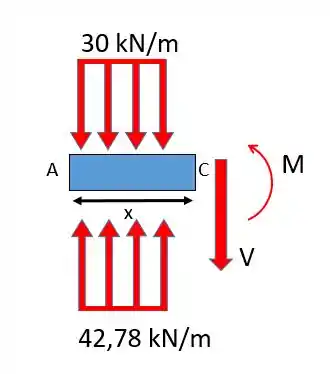
Veja que apareceram os termos da força cortante e do momento fletor . Outra coisa importante é que essa seção pode ser feita em qualquer posição entre A e C, logo consideramos uma distância , sendo e .

Agora vamos aplicar as condições de equilíbrio:

Para o momento:

Aqui a gente tem que lembrar que o momento de uma força distribuída é calculado da seguinte forma: Calcula-se a força concentrada equivalente e faz essa força aplicada ao centro geométrico da distribuição (neste caso na metade porque é uma distribuição constante, um retângulo).

obs: Para conferir você sempro pode derivar em relação à , se der diferente de é algo de errado não está certo. No nosso caso dá certinho então, provavelmente, acertamos =D

Seção CD:

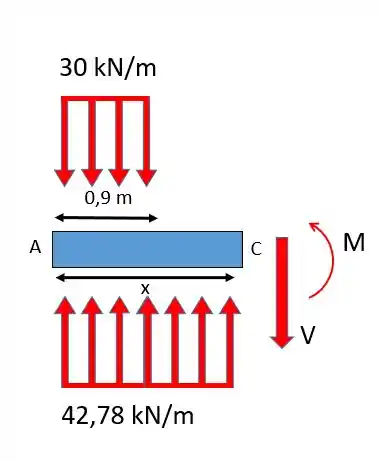
Agora a gente avançou para a seção seguinte, perceba que sempre o tamanho da nossa seção vai ser , mas aqui a carga distribuída de só vai até , isso é importante!

Aplicando as equações de equilíbrio:

para o momento:

Novamente a derivada de em função de é igual a .

Seção DE:

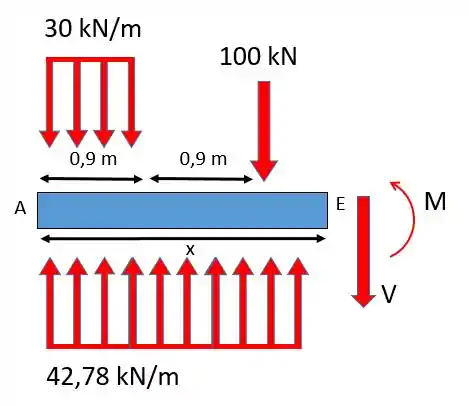
Aplicando as equações de equilíbrio:

para o momento:

Novamente a derivada de em função de é igual a .

Finalmente a seção EB:

Aplicando as equações de equilíbrio:

para o momento:

Novamente a derivada de em função de é igual a .

Agora a gente pode fazer o gráfico Com todas as seções:

AC:

CD:

EE:

EB:

Vamos representar os diagramas com base em suas equações apresentando apenas os resultados nos pontos de transição, assim como os máximos e mínimos.

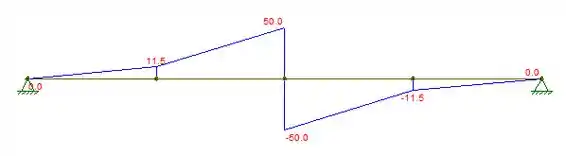
Logo a diagrama de força cortante ficará da seguinte forma:

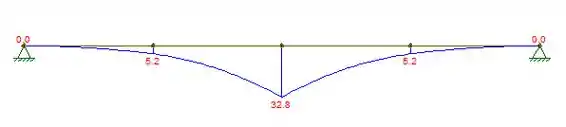
E o do momento fletor:

Pelo diagrama é possível ver que a força cortante máxima ocorre na metade da barra e vale .

Já o momento fletor máximo vale e também ocorre na metade da barra.