Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 70

Um automóvel desloca-se para a direita com uma velocidade constante de 80 km/h. Se o diâmetro da roda é de 500 mm, determine as velocidades dos pontos B, C, D e E sobre o aro da roda.

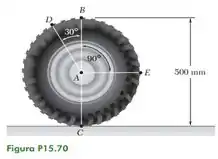
Passo 1

E aí meus caros! Bora pra questão 70 agora!

Bom! A gente quer determinar as velocidades nos pontos B , C , D e E da roda.

O enunciado nos diz que o automóvel desloca-se para a direita com uma velocidade constante de 80   k m / h . Essa é a velocidade do centro de massa. Logo;

v A = 80   k m / h

Passando pra m / s :

v A = 80 3,6   m / s = 22,22   m / s

Agora, vamos fazer um esboço da distribuição de velocidades na roda nos quatro pontos de interesse...

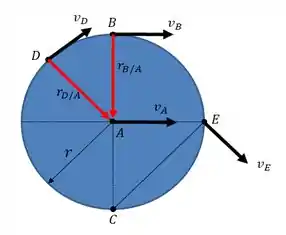
Passo 2

Bom! A gente sabe que o raio da roda é dado por...

r = 500   m m 2 = 250   m m

r = 0,25   m

E a roda gira com uma velocidade angular igual à...

ω = v A r = 22,22   m / s 0,25   m

ω = 88,88   r a d / s

Como os vetores posição em relação a A , são todos iguais...

r B / A = r C / A = r D / A = r E / A = r

Então,

v B / A = v C / A = v D / A = v E / A = ω r

v B / A = v C / A = v D / A = v E / A = 22,22   m / s

Só que essas velocidades vão estar distribuídas assim, na roda...

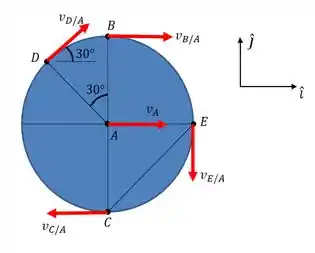
Passo 3

Assim, é só calcular as as velocidades!

A velocidade v D vai ser dada por...

v → D = v → A + v → D / A

v → D = 22,22 i ^ + 22,22 cos ⁡ 30 ° i ^ + 22,22 sen ⁡ 30 ° j

v → D = 41,46 i ^ + 11,11 j ^

v D = 42,93   m / s   ∠ 15 °

Já a velocidade v B ...

v → B = v → A + v → B / A

v → B = 22,22 i ^ + 22,22 i ^

v → B = 44,44 i ^

v B = 44,44   m / s →

v C vai ser igual à...

v → C = v → C + v → C / A

v → C = 22,22 i ^ - 22,22 i ^

v → C = 0 i ^

v C = 0  

E por último, falta obter v E :

v → E = v → E + v → E / A

v → E = 22,22 i ^ - 22,22 j ^

v E = 31,42   m / s   ∠ - 45 °

Pronto! Missão cumprida!

Resposta

v B = 44,44   m / s →

v C = 0   m / s

v E = 31,42   m / s   ∠ - 45 °

v D = 42,93   m / s   ∠ 15 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.49. No sistema de engrenagens planetárias mostrado na figura, o raio da engrenagem central A é a, o raio das engrenagens planetárias é b e o raio da engrenagem externa E é a +-2b. A velocidade angu
15.51. O braço AB gira com uma velocidade angular de 20 rad /s no sentido anti-horário. Sabendo que a engrenagem C é estacionária, determine (a) a velocidade angular da engrenagem B, (b) a velocidade
15.51. O braço AB gira a uma velocidade angular de 42 rpm no sentido horário. Determine a velocidade angular requerida da engrenagem A para que (a) a velocidade angular da engrenagem B seja de 20 rpm
15.50. A engrenagem A gira com uma velocidade angular de 120 rpm no sentido horário. Sabendo que a velocidade angular do braço AB é 90 rpm no sentido horário, determine a velocidade angular correspond
15.54. O braço ACB gira em torno do ponto C com velocidade angular de 40 rad /s no sentido anti-horário. Dois discos de atrito A e B estão presos por pinos em seus centros ao braço ACB do modo mostrad