Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 102

Usando o método da Seção 15.7, resolva o Problema 15.64.

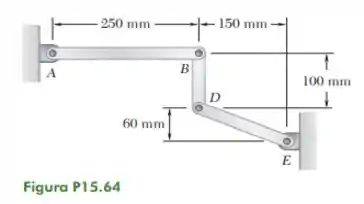
Passo 1

E aí meus caros! Simbora pra mais uma questão do Beer!

Bom! A gente quer determinar as velocidades angulares das barras B D e D E !

É uma questão bem parecida com a do item anterior! Como em time que tá ganhando não se mexe, vamos usar o mesmo procedimento... O dos versores!

E novamente iremos usar os versores i ^ , j ^ e k ^ ... Onde logo abaixo, está mostrada a situação em que devemos usá-los...

i ^ → E i x o   x

j ^ → E i x o   y

k ^ → S e n t i d o   d e   r o t a ç ã o   ( - k ^   p a r a   o   h o r á r i o   e   k ^   p a r a   o   a n t i - h o r á r i o )

Feshow!? Agora, vamos posicionar um eixo de coordenadas naquela figura do enunciado...

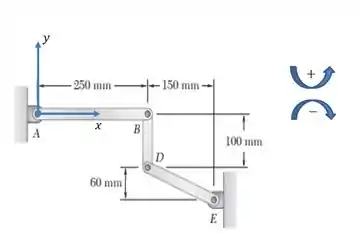
Outra coisa que é importante saber também, é a tabela de produto vetorial entre versores...

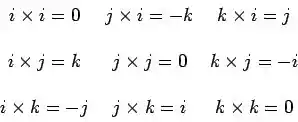
Passo 2

Vamos começar pela barra A B . A barra está girando a 4   r a d / s no sentido horário. Logo...

ω A B = 4   r a d / s ⤾   = ( 4   r a d / s ) ( - k ^ )

ω → A B = - 4 k ^   r a d / s

E o vetor de posição de B em relação a A , é dado por...

r → B / A = ( 250   m m ) ( - i ^ )

r → B / A = - 250 i ^   m m

Logo, a velocidade em B , uma vez que A está fixo, ou seja, só tem rotação... Vai ser dada por:

v → B = ω → A B × r → A B

v → B = ( - 4 k ^   r a d / s ) × ( - 250 i ^   m m )

v → B = ( 1000   j ^ )   m m / s = 1 j ^   m / s

Passo 3

Em seguida, vamos partir pra barra B D . A velocidade angular dela, que ainda não sabemos, é dada por...

ω → B D = ω B D k ^

E a velocidade em D vai ser dada pela soma da translação em B   mais rotação sobre B ...

v → D = v → B +   ω → B D × r → D / B

Como o vetor posição de D pra B é dado por...

r → D / B = ( 100 j ^   m m )

r → D / B = 100 j ^   m m = 0,1 j ^   m

Desse modo...

v → D = v → B +   ω → B D × r → D / B

v → D = 1 j ^   + ω B D k ^ × ( 0,1 j ^   m )

v → D = ( 1 j ^ - 0,1 ω B D i ^ )   m / s

Passo 4

Continuando nosso raciocínio, vamos agora barra D E . A velocidade angular dela, que ainda não sabemos, é dada por...

ω → D E = ω D E k ^

Como a velocidade vai ser dada apenas pela rotação, já que E está fixo. Podemos determinar a velocidade em D como...

v → D = ω → D E × r → D / E  

Como o vetor posição de D pra E é dado por...

r → D / E = 150 i ^ - 60 j ^   m m

r → D / B = 0,150 i ^ - 0,0 60 j ^   m

Desse modo...

v → D = ω → D E × r → D / E  

v → D = ω D E k ^ × [ 0,150 i ^ - 0,0 60 j ^   m ]

v → D = 0,150 ω D E j ^ + 0,0 60 ω D E i ^   m / s

Passo 5

Agora, é só uma questão de igualar as velocidades em D que obtivemos nos P a s s o s 3 e 4 ...

v → D = ( 1 j ^ - 0,1 ω B D i ^ )   m / s = 0,150 ω D E j ^ + 0,0 60 ω D E i ^   m / s

Relacionando as partes com os mesmos versores. Em j ^ , temos que...

1 = 0,150 ω D E

ω D E = 1 0,150

ω D E = 6,67   r a d / s   ⤿

Em i ^ , por sua vez...

- 0,1 ω B D = 0,0 60 ω D E

ω B D = - 0,06 0,1 ω D E

ω B D = - 0,06 0,1 ⋅ ( 6,67   r a d / s )

ω B D = - 4   r a d / s

ω B D = 4   r a d / s   ⤾

Quando o sinal dá negativo, é porque a barra gira no sentido horário! Quando dá positivo, é porque o sentido é anti-horário! Isso segundo a convenção que adotamos!

Pronto! Conseguimos obter as velocidades angulares de B D e D E !

Bora pra frente que atrás vem gente!

Resposta

ω B D = 4   r a d / s   ⤾

ω D E = 6,67   r a d / s   ⤿

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra uniforme de 20k g é liberada a partir do repouso na posição horizontal mostrada e atinge o canto fixo B no centro de percussão da barra. Determine a componente t da força exercida pelo mancal
A barra semicircular uniforme de massa m e raio r é livremente articulada em torno de um eixo horizontal através de A . Se a barra é liberada a partir do repouso na posição mostrada, onde A B é horizo
Para o Prob. 6 / 46 , determine a componente na direção n da força exercida pelo mancal em O um instante antes do impacto da barra com a quina B .
A placa retangular uniforme é liberada a partir do repouso na posição mostrada. Determine o valor de x para o qual a aceleração angular é máxima, e determine a aceleração angular correspondente. Compa
Um teste de vibrações é realizado para verificar a adequação do projeto dos mancais A e B . O rotor desbalanceado e o eixo incorporado possuem uma massa combinada de 2,8k g . Para determinar a posição