Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 28
Um avião a jato com uma velocidade de aterrissagem de reduz sua velocidade para por meio de um empuxo negativo proveniente de seus reversores de empuxo, em uma distância de ao longo da pista de pouso com desaceleração constante. A massa total da aeronave é de com o centro de massa em . Calcule a reação sob a roda dianteira próximo do final do intervalo de frenagem e antes da aplicação do freio mecânico. Na velocidade mais baixa, as forças aerodinâmicas sobre a aeronave são pequenas e podem ser desprezadas.
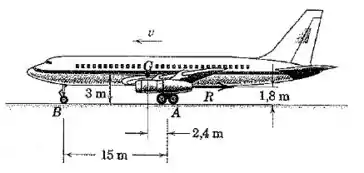
Passo 1
Vamos começar calculando a deaceleração do avião, sabendo que ele reduz sua velocidade de para ao longo de uma distância de :
Passo 2
Usando essa aceleração, podemos calcular o momento da força resultante que age no centro de massaa. Vamos fazer esse cálculo em relação a um ponto que anule o momento das forças desconhecidas, precisamos de um desenho para achar esse ponto:
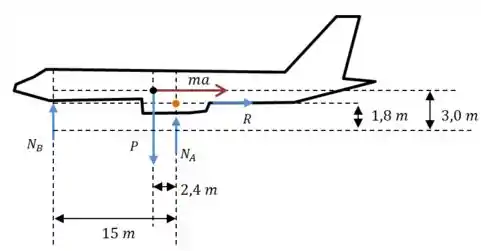
Se escolhermos o ponto laranja (vamos chamá-lo de ), os momentos de e de se anulam, e então podemos escrever o seguinte:
Resposta
A reação normal sobre a roda dianteira é de .