A caminhonete carregada, que possui uma massa de com centro de massa em , está puxando o reboque de com centro de massa em . Enquanto desce uma inclinação de , o motorita aciona os freios e diminui a velocidade de para em uma distância de . Para esse intervalo, calcule as componentes e da força exercida sobre o engate do reboque em pela caminhonete. Encontre também a força normal correspondente sobre cada par de rodas em e . Despreze o efeito da rotação das rodas.
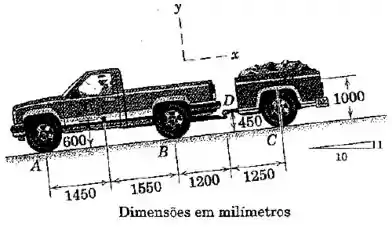
Passo 1
Se a inclinação é de , o ângulo que o plano inclinado forma com a horizontal é:
E se o sistema diminui sua velocidade de (ou ), para () em uma distância de , a sua aceleração (se for consante) é:
(Na figura, o sentido positivo de é contrário ao movimento, por isso nesse processo de desaceleração).
E então podemos calcular as forças resultantes que agem sobre a caminhonete e sobre o reboque.
Passo 2
Beleza, nosso objetivo é encontrar as forças normais e que agem nas rodas, e a força no reboque em .
Já vimos que o reboque tem uma aceleração no sentido negativo do eixo . Quais as forças que agem nessa direção?
Onde é a componente em da força no reboque em :
E podemos usar uma equação de momentos para calcular a componente vertical dessa força. Vamos tomar o ponto como referência, assim anularemos a força no pneu do reboque.
A soma dos momentos das forças tem que ser igual ao momento da força resultante agindo no centro de massa:
E a distância perpendicular entre o centro de massa e o ponto é :
E quais os momentos das forças em relação ao ponto ? está a , está a e o peso está a (favorecendo a rotação no sentido contrário), então:
Passo 3
E para encontrar a força normal na roda do reboque, vamos aplicar a segunda lei de Newton sobre o reboque na direção :
Passo 4
E agora só falta encontrar a força na roda da caminhonete. Vamos aplicar uma equação de momentos sobre ela, tomando o ponto como referência, já que não conhecemos a força , e nem queremos conhecer.
Olhando para o desenho, vemos que o torque da força resultante em relação a esse ponto é:
Vamos tomar o sentido horário como positivo.
Ok, isso tem que ser igual à soma dos torques das outras forças. Vamos começar pelas duas componentes da força peso:
E agora as duas componentes da força em :
E por mim o da força que queremos calcular:
Agora é só resolver a equação:
Resposta
As componentes da força sobre o engate são e e as forças sobre as rodas são e .