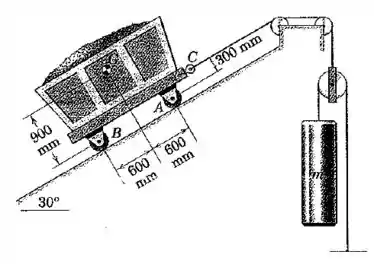
Determine a massa máxima do cilindro para a qual o vagão de carvão carregado com não irá tombar com relação às rodas traseiras . Despreze a massa de todas as polias e rodas. (Note que a tração no cabo em não é .)

Estamos em busca de duas variáveis, então temos que montar duas equações.

Vamos começar com uma equação de momentos. Ainda pensando no caso limite, em que a roda está prestes a perder contato com o chão em . Vimos que o carrinho tem aceleração , então:

Onde é a distância perpendicular entre o centro de massa e o ponto de referência que escolhermos:

é nula no nosso caso limite, e e são desconhecidas. Como queremos calcular , vamos colocar nosso ponto de referência em , e então:

Onde estamos tomando o sentido horário como positivo, já que a nossa aceleração aponta no sentido que sobe o plano (e age no centro de massa).

E os momentos dessas forças em relação ao ponto são:

Agora é só igualar:

Essa é nossa primeira equação.

Agora vamos encontrar a segunda equação usando a segunda lei de Newton.

E estamos aplicando essa equação na direção paralela à superfície do plano, que é a direção da aceleração , da componente do peso, e da tração :

E vamos substituir a equação que encontramos para no passo anterior:

E como :

E substituindo isso em uma das equações, podemos calcular a tração:

Agora é só substituir na nossa fórmula do passo para encontrar a massa do cilindro: