Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 27
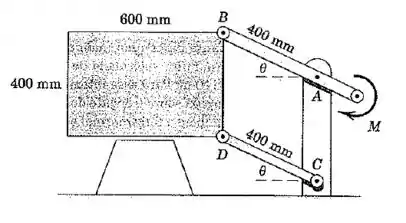
A placa retangular homogênea de é apoiada no plano vertical pelas hastes leves paralelas mostradas. Se um momento é aplicado à extremidade da haste com o sistema inicialmente em repouso, calcule a força suportada pelo pino em quando a placa se desprende do seu suporte com .
Passo 1
Vamos começar olhando apenas para a haste . No instante em que a placa se desprende do suporte, o momento total sobre essa haste deve ser próximo de zero:
Onde tomamos o ponto como referência por conveniência, mas isso seria verdadeiro para qualquer outro ponto.
Além do momento agindo na extremidade da barra, temos uma componente (tangencial) da força que a placa faz sobre a haste gerando momento no sentido oposto, então:
Passo 2
Agora vamos olhar apenas para a placa. Além da reação a , a única outra força agindo na direção tangencial, no instante em que a placa se desprende do suporte, é a componente da força peso:
E com isso já podemos calcular a aceleração tangencial do sistema:
Passo 3
E com essa aceleração, podemos calcular o momento da força resultante, agindo no centro de massa do sistema.
Onde escolhemos o ponto para que ficássemos apenas com e na expressão do momento.
A distância perpendicular entre a força e o ponto é , e para a força a distância é , então:
E para calcular o momento da força resultante temos que considerar suas duas componentes:
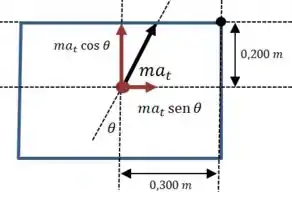
Agora vamos igualar as duas expressões:
Que, como vimos antes, é igual à força suportada pelo pino em no instante em que a placa perde o contato com o suporte.
Resposta
A força suportada é de .