A chapa de aço uniforme de é livremente articulada em torno do eixo como mostrado. Calcule a força suportada por cada um dos mancais em e imediatamente após a chapa ser liberada a partir do repouso no plano horizontal -.
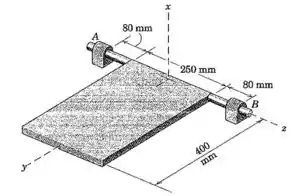
Passo 1
A força peso irá gerar um momento que dará uma aceleração angular para a placa em torno do eixo .
O momento dessa força que age no centro de massa da placa em relação a esse eixo é:
E para calcular a aceleração angular gerada por esse momento, precisamos saber o momento de inércia da chapa retangular uniforme em relação a um eixo perpendicular ao sei maior lado (consultar tabela):
Então:
Passo 2
Essa é a aceleração angular imediatamente após a chapa ser liberada. Conforme ela roda em torno de , o ângulo que a força peso forma com a superfície da placa muda, e portanto o momento também.
Mas nesse instante, podemos calcular a aceleração tangencial associada a essa aceleração angular:
Onde é a distância entre o eixo e o centro de massa da placa, que nesse instante acelera na vertical para baixo:
Passo 3
Então temos o seguinte sistema:
Temos um sistema de três variáveis, e duas equações, então precisamos encontrar mais uma das variáveis antes de resolvê-lo.
Olhando para a parte de cima do veículo, vamos aplicar a segunda lei de Newton na direção horizontal, que é justamente a direção da aceleração .
Apenas a força aponta nessa direção, no mesmo sentido da aceleração :
Substituindo isso no sistema:
Podemos resolver para calcular . Vamos multiplicar a equação de baixo por e somar com a primeira:
Passo 4
Isso quer dizer que, no instante que estamos analisando, a aceleração do centro de massa da placa é na vertical para baixo.
Então pela segunda lei de Newton:
E nessa direção temos forças de módulo agindo em cada mancal ( e ), e a força peso apontando para baixo:
Resposta
A força suportada por cada um dos mancais é .