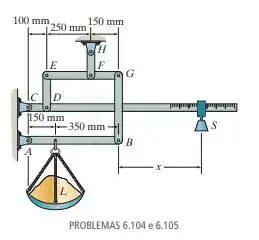
A balança de plataforma consiste em uma combinação de alavancas de terceira e primeira classes, de modo que a carga sobre uma alavanca se torna o esforço que move a próxima alavanca. Por meio desse arranjo, um pequeno peso pode equilibrar um objeto pesado. Se e a massa do contrapeso S é 2 kg, determine a massa da carga L necessária para manter o equilíbrio.

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, para equilíbrio da barra

Logo:

Esta força pode ser levada diretamente à barra Logo, para equilíbrio de

Agora, aplicando o somatório de forças na barra para descobrir a força em

Substituindo:

Por fim, basta encontrar o valor de que equilibra a barra que vai de até depois de Logo:

Substituindo os valores de e das forças e isolando

Prontinho, o peso que mantém o equilíbrio é