Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 77
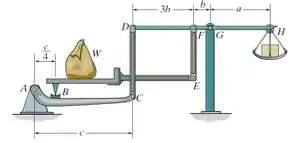
Mostre que o peso do contrapeso em necessário para o equilíbrio é e, portanto, ele é independente da posição da carga na plataforma.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Para esta questão basta obtermos a relação . É tão bom começar uma questão já sabendo a resposta...
Como vocês podem observar na questão, a nossa estrutura é composta por várias barras. A ideia para resolvermos a questão é dividir para conquistar.
Então, vamos dividir a estrutura em três partes principais: a barra , a barra e a barra . Somente fazendo esta divisão vamos conseguir resolver a nossa questão.
Sendo assim devemos esboçar o diagrama de corpo livre para os três membros. Só devemos tomar muito cuidado ao colocarmos forças que aparecem em dois componentes! Pela lei de ação e reação, elas terão um sentido oposto!
Sendo assim, para a barra , temos:
Percebam que o peso foi colocado em um ponto qualquer! Inclusive, para deixar mais evidente isto, nem as dimensões foram indicadas! Continuando, para a barra , temos:
E por fim, para a barra , temos:
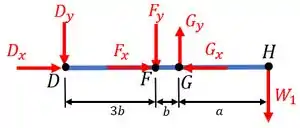
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Vamos começar a nossa questão trabalhando com a barra .
Aqui a nossa análise é bem simples. Pela barra estar em equilíbrio, o somatório de forças na vertical deve ser igual a zero. Portanto,
Vamos guardar esta relação para utilizar nos próximos dois Passos!
Passo 3
Agora já podemos partir para a barra . Aqui nosso objetivo é descobrir a força .
Para isto, devemos fazer o somatório de momentos em torno do ponto . Sendo assim, temos:
Antes de pararmos por aqui, vamos aproveitar para identificar quem são as forças no pino em .
Como a barra é uma barra simples, com um único elemento e forças apenas nos pinos, então, a força no pino é exatamente as do pino , a diferir apenas do sentido.
Logo, e .
Passo 4
E para finalizarmos a questão, basta analisar a barra .
Para que a gente obtenha a relação , basta fazermos o somatório dos momentos em torno do ponto . Sendo assim, temos:
Substituindo as relações de e que descobrimos nos Passos anteriores, temos:
E assim finalizamos a questão!