Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 104
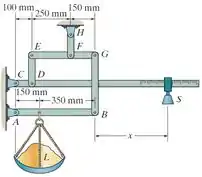
A balança de plataforma consiste em uma combinação de alavancas de terceira e primeira classes, de modo que a carga sobre uma alavanca se torna o esforço que move a próxima alavanca. Por meio desse arranjo, um pequeno peso pode equilibrar um objeto pesado. Se , determine a massa do contrapeso necessária para equilibrar uma carga de 90 kg.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Devemos determinar a massa do contrapeso localizado quando .
Como vocês podem observar na questão, a nossa estrutura é composta por várias barras. A ideia para resolvermos a questão é dividir para conquistar.
Então, vamos dividir a estrutura em três partes principais: a barra , a barra e a barra . Somente fazendo esta divisão vamos conseguir resolver a nossa questão, pois é fundamental descobrir qual a força no pino para que calculemos a massa do contrapeso.
Ah, mas e as barras e ??? Bom, vamos precisar sim ao decorrer da questão, mas não será necessário esboçarmos o diagrama delas, por serem barras simples.
Sendo assim devemos esboçar o diagrama de corpo livre para os três membros. Só devemos tomar muito cuidado ao colocarmos forças que aparecem em dois componentes! Pela lei de ação e reação, elas terão um sentido oposto!
Sendo assim, para a barra , temos:
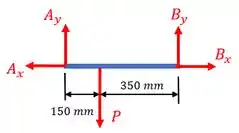
Sendo o peso da carga . Já para a barra , temos:
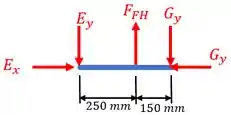
E por fim, para a barra , temos:
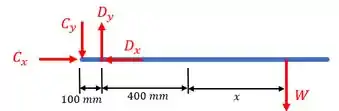
Sendo o peso do contrapeso. Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Vamos começar a nossa questão trabalhando com a barra (a única que conhecemos algum valor de força).
O objetivo aqui é apenas determinar quem é , pois esta será a única força que afetará no contrapeso, o que veremos ao decorrer da questão!
Portanto, para calcularmos quem é , basta fazermos o somatório dos momentos em torno do ponto , pois assim teremos como única incógnita . Então,
Passo 3
Agora já podemos partir para a barra . Mas, antes de analisarmos ela, vamos considerar aqui quem são as forças em .
As forças em são exatamente as forças no pino em , a diferir apenas do sentido (como mostrado nos diagramas). Portanto, e (não que a gente precise deste último).
Agora sim podemos continuar! Novamente, nosso único objetivo será calcular . Fazendo o somatório dos momentos em torno do ponto , temos:
Passo 4
E para finalizarmos a questão, basta analisar a barra .
Assim como ocorreu com a força em , visto no Passo 3, também ocorrerá com . Logo, e .
Como queremos descobrir quem é a massa do contrapeso, basta calcularmos o somatório de momentos em torno do ponto . Portanto,
E assim finalizamos a questão! Viram que só precisava da força no nosso primeiro diagrama?!