Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 38
Determine a força nos membros e da treliça . Indique se os membros estão sob tração ou compressão. Dica: use as seções e .
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
Nesta questão vamos fazer algumas manipulações com as equações de equilíbrio. Portanto fique bem atento ao diagrama de corpo livre.
Primeiro devemos construir um diagrama de corpo livre e descobrir o valor das reações de apoio. Temos que:
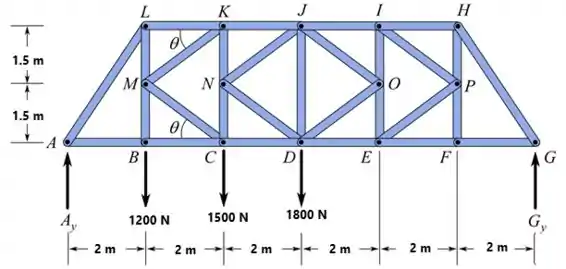
Passo 2
Pela geometria
Equilibre os momentos sobre o ponto G
Passo 3
Vamos desenhar o nosso D.C.L da treliça para a esquerda da seção .
Onde
é a força de tração no membro JK,
é a força de compressão no membro CD,
é a força de compressão no membro CN,
é a força de compressão no membro KN.
Passo 4
Equilibre os momentos sobre a junta C
Portanto, a força no membro JK é de .
Vamos agora equilibrar as forças na direção horizontal,
Portanto, a força no membro CD é de (C).
Vamos desenhar o nosso D.C.L da treliça para a esquerda da seção .
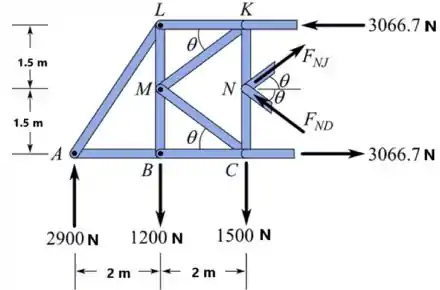
Passo 5
Vamos equilibrar as forças na direção horizontal,
Vamos equilibrar as forças na direção vertical,
Substituindo a expressão (1)
Substituindo
Portanto, a força no membro ND é de (C).
Portanto, a força no membro NJ é de (T).
Resposta
Portanto, a força no membro JK é de .
Portanto, a força no membro CD é de (C).
Portanto, a força no membro ND é de (C).
Portanto, a força no membro NJ é de (T).