Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 90
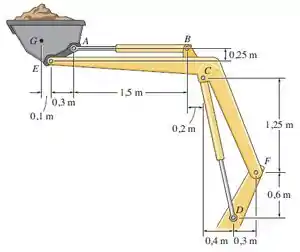
A lança do trator suporta a massa uniforme de 600 kg na caçamba, que tem um centro de massa em . Determine as forças em cada cilindro hidráulico, e , e as forças resultantes nos pinos e . A carga é suportada igualmente em cada lado do trator por um mecanismo semelhante.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar as forças em cada cilindro hidráulico, e e nos pinos e . É tanta informação que precisamos determinar que devemos tomar cuidado para não nos perdermos!
Vamos começar esboçando o diagrama de corpo livre de toda a lança do trator, apenas substituindo os pontos e pelas suas reações. Desta forma, temos:
Passo 2
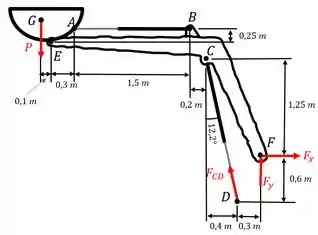
Vamos calcular agora a força no cilindro e as reações em (metade do que a questão nos pede. Fazendo o somatório dos momentos em torno de , temos:
Já para calcularmos as componentes da força no pino basta fazermos o somatório de forças em ambas as direções. Portanto,
Resolvendo o sistema acima obtemos:
E portanto, a reação no pino será:
Passo 3
Para finalizarmos a questão temos que determinar a força no cilindro e no pino E. Para isto, vamos analisar o diagrama de equilíbrio apenas da caçamba.
Esboçando este diagrama, teremos:
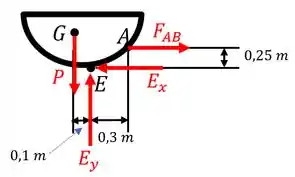
Portanto, para obtermos a força do cilindro hidráulico em basta fazermos o somatório de momentos em torno do ponto . Logo,
Já para descobrirmos as forças no pino , basta analisarmos o somatório de forças na direção vertical e horizontal. Portanto,
Do sistema acima obtemos que e . E portanto, a reação no pino será:
E assim finalizamos a questão!