Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas Revisão - Ex. 159
Uma barra de alumínio fundido é feito de uma liga em que e . Sabendo-se que a intensidade T dos torques aplicados é gradual e crescente e usando o critério de Mohr, determinar a tensão de cisalhamento para que possa ser esperada a ruptura.
Passo 1
Para resolver o nosso problema usando o critério de Mohr? Para isso precisamos analisar as tensões que agem no nosso elemento.
Sabemos que pelo critério de Mohr, podemos escrever um gráfico em função das tensões limites que agem no nosso elemento.
Com isso, podemos escrever o nosso gráfico da seguinte maneira:
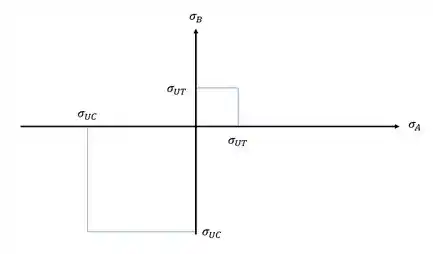
De maneira conservadora podemos ligar os pontos, sendo assim teremos que os limites de tensões são dados por.
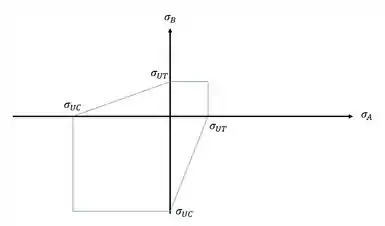
Se temos os limites de tensões que a nossa estrutura está submetida, vamos determinar as tensões que agem na nossa estrutura.
Quando tivermos essas tensões, poderemos usar a seguinte relação para determinação da tensão cisalhante máxima que pode agir na nossa estrutura:
Passo 2
Como a nossa barra está submetida apenas a um torque, sabemos que o torque produz apenas tensões cisalhantes na nossa estrutura, sendo assim já sabemos de antemão que:
Sabemos que a tensão média vai ser dada por:
Da mesma forma, podemos determinar o valor de pela seguinte equação:
E porque fizemos isso? Porque queremos determinar as tensões máximas, com isso vamos ter que:
Substituindo na equação teremos que:
Sendo assim a nossa tensão cisalhante vai ser dada por:
E perceba que esses valores temos no osso enunciado, sendo assim teremos que: