Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 148b
Nós expressamos por , e as três medidas de deformação específica normal feitas com uma roseta à 60°. Pede-se (b) Sabendo-se que as seguintes medidas foram feitas com esta roseta, em um dado ponto de um componente de máquina, determinar, neste ponto, as deformações específicas normais, no plano, e a máxima deformação específica de cisalhamento, no plano.
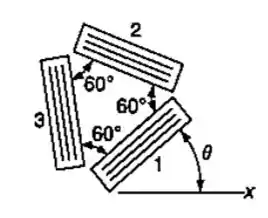
Passo 1
Essa parte do problema nos fornece os dados de deformação da roseta, com isso é possível achar as deformações , e . Com essas deformações a gente vai fazer o nosso ciclo de Mohr para deformação e achar a máxima deformação específica de cisalhamento e normal =D
Passo 2
As equações que vamos utilizar são da seguinte forma, onde o ângulo é o ângulo da roseta.
Daí é só substituir, aqui o ângulo do desenho não vai mudar nada, exatamente pelo que foi descrito na letra A, então vamos considerar
Para
Para
Para
Desta forma a gente obtém um sistema:
Passo 3
Para resolver este sistema primeiro a gente substitui nas duas últimas equações:
Obtendo:
Agora a gente vai somar as duas equações:
Para achar vamos subtrair a segunda da primeira:
Portanto achamos:
Passo 4
Vamos fazer então o ciclo de Mohr para deformações. Para isso a gente tem que lembrar como calcula a deformação específica normal média e o raio:
Perceba que é muito parecido com o ciclo de Mohr com as tensões mas aqui utilizamos:
- que é a deformação específica normal.
- que é a deformação angular.
utilizando os cálculos do passo 1:
E
Agora podemos desenhar o ciclo de Mohr:
Passo 5
Para calcular a intensidade dessas deformações específicas normais principais temos que calcular e . Como já temos a média o o raio fica fácil:
Passo 6
A máxima deformação específica de cisalhamento no plano é obtida, também, pelo ciclo de Mohr e é igual ao raio a duas vezes o raio:
Resposta
b)