Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 148a
Nós expressamos por , e as três medidas de deformação específica normal feitas com uma roseta à 60°. Pede-se (a) mostrar que a soma destas deformações e a soma do quadrado de suas diferenças são ambas independetes da orientação da roseta, e respectivamente iguais a:
e
Onde é a abcissa do centro do círculo de Mohr para as correspondentes deformações e é o raio deste círculo.
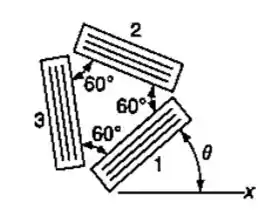
Passo 1
Vamos lá galera, este é um problema bem teórico então vai exigir um pouco mais de abstração da nossa parte, mas para facilitar um pouco e tentar tornar um pouco mais concreto vamos pegar o círculo de Mohr para um caso onde existam três deformações. Vai ficar assim:
Passo 2
As equações que vamos utilizar são da seguinte forma:
Uma das coisas mais funcamentais dessa questão é achar os ângulos . Eles vão ser:
Daí é só substituir:
Para
Para
Para
Agora vamos utilizar algumas propriedades trigonométricas de soma de seno e cosseno para os casos 2 e 3, da seguinte forma:
Continuaremos no passo 3.
Passo 3
Agora que relembramos a soma dos ângulos podemos determinar os valores para :
E para :
Observe que a gente não ta substituindo os valores pra não ficar mais confuso ainda! Mas o que podemos fazer é lembrar que:
Dessa forma a gente pode passar tudo para 60° de modo a facilitar um pokito!
para :
E para a gente mantém a mesma coisa de antes:
Passo 4
Vamos só lembrar que o problema pede, essencialmente, para calcularmos . Vamos fazer isso com bastante calma então nós temos:
Para () a gente já achou uma substituição legal, antes era assim:
Com a substituição trigonométrica do passo anterior fica:
Aí, galera daqui pra gente o problema se torna apenas algébrico então vou ajudar vocês um pouco porque vamos ter que substituir os valores de e e ainda elevar tudo ao quadrado vamos ter no final o seguinte:
Para vamos ter:
Passo 5
Lembra dessa equação?
Então pessoal, a gente já calculou uma porrada de coisa então aqui vai o pulo do gato nessa questão que é somar com com :
Gente, eu coloquei esses ’s só porque a equação iria ficar muito gigante, na verdade eles valem:
Aí se a gente substituir esses valroes dos senos e cossenos pelos valores calculados no passo anterior a gente vai ver que:
Então a gente vai ter:
Como
Prontinho!!
Passo 6
Para achar a segunda relação:
A gente vai fazer a mesma coisa, vamos substituir os valores da deformação pelas equações em função dos ângulos .
A única coisa a mais que a gente precisa saber é que
E como a gente viu no passo anterior , Logo:
Resposta
Ei, a resposta está no passo a passo :)