Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas Revisão - Ex. 157

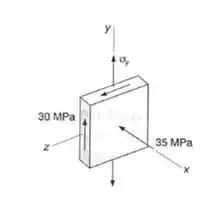
Para o estado de tensões mostrado, determinar a máxima tensão de cisalhamento, quando:

  1. σ y = + 80   M P a
  2. σ y = - 80   M P a

Passo 1

Para resolver esse tipo de questão, temos que conhecer um pouco sobre o estado triaxial de tensões, o que vai facilitar em muito a nossa vida na hora de calcular o nosso objetivo, que é determinar a tensão máxima de cisalhamento.

Para fazer isso, é muito simples, pensa em um circulo de mohr que representasse as tensões principais em mais de uma direção, se formos pensar nele assim, sabemos que ele vai ter a seguinte cara:

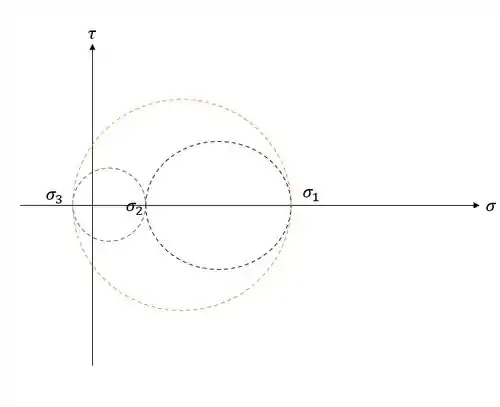
Sabemos que o raio da maior circunferência é exatamente a máxima tensão cisalhante que ocorre no nosso elementinho, e podemos calcular o raio da circunferência da seguinte maneira:

τ M a x = σ 1 - σ 3 2

E sabemos que as tensões σ 1   e   σ 3 são tensões principais, ou seja, que ocorrem em planos sem tensão cisalhante.

Com todas essas informações, já podemos resolver o nosso problema, vamos nessa?

Passo 2

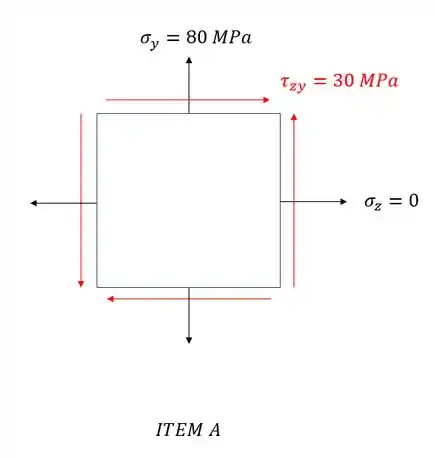
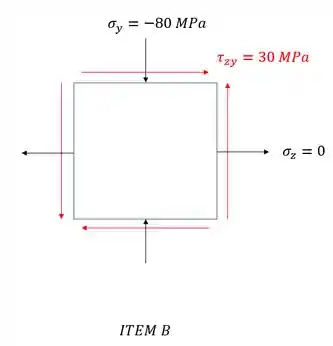
Olhando o nosso elemento finito, temos que os dois casos dados são:

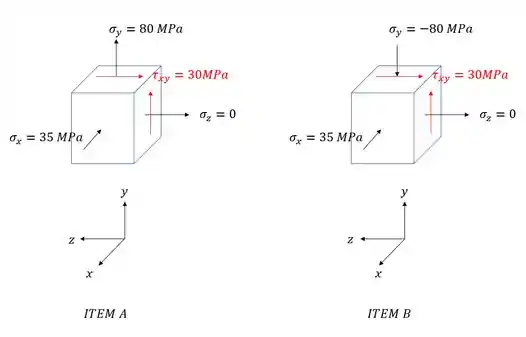
Perceba que a tensão em x é - 35 M P a , e que os planos perpendiculares a direção x não possuem tensões cisalhantes, ou seja, a tensão em x já é uma tensão principal, mas não sabemos qual das 3, sendo assim temos que:

σ x = - 35   M P a σ 1 σ 2 σ 3

Para sabermos exatamente quais as tensões principais totais, precisamos calcular as tensões principais do outro plano, com isso temos a seguinte situação:

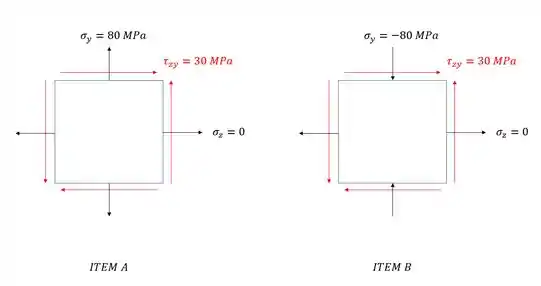
Como nosso objetivo agora é determinar as tensões principais, temos as seguintes equações pra isso:

σ 1 = σ m e d + R

σ 2 = σ m e d - R

Sabemos que:

σ m e d = σ z + σ y 2

R = σ z - σ y 2 2 + τ z y 2

Com isso vamos ter que:

  1. σ y = 80 M P a

    2. Substituindo temos que:

    σ m e d = σ z + σ y 2 = 0 + 80 2 = 40   M P a

    R = 0 - 8 0 2 2 + 30 2 = 50   M P a

    σ 1 = σ m e d + R = 40 + 50 = 90   M P a

    σ 2 = σ m e d - R = 40 - 50 = - 10   M P a

    Assim temos que:

    σ 3 = - 35   M P a

    Ou seja, se montarmos o nosso círculo, teremos que:

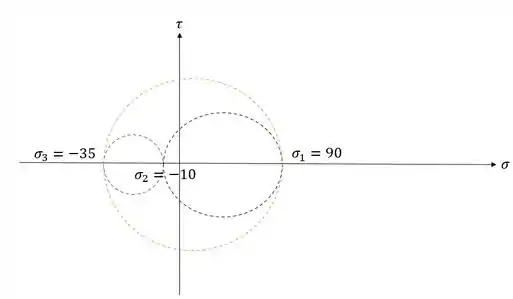
    Calculando o raio, teremos que:

    τ M a x = 90 - ( - 35 ) 2 = 62,5   M P a

  2.   σ y = - 80   M P a

Substituindo temos que:

σ m e d = σ z + σ y 2 = 0 + ( - 80 ) 2 = - 40   M P a

R = 0 - ( - 80 ) 2 2 + 30 2 = 50 M P a

σ 1 = σ m e d + R = - 40 + 50 = 10   M P a

σ 2 = σ m e d - R = - 40 - 50 = - 90   M P a

Colocando em ordem teremos que:

σ 1 = 10   M P a

σ 2 = - 35   M P a

σ 3 = - 90   M P a

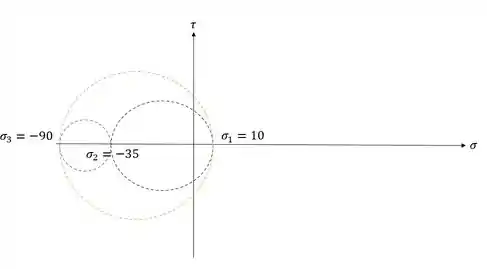
Calculando o raio, teremos que:

τ M a x = 10 - ( - 90 ) 2 = 50   M P a

Resposta

  1. τ M a x = 62,5   M P a

  2. τ M a x = 50 , 0   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque de ar comprimido AB tem um diâmetro externo de 462 m m e uma espessura uniforme e 6 m m . Sabendo-se que a pressão dentro do vaso é de 130k P a , determinar a máxima tensão normal e a máxima
Um cabo de aço de 18 m de comprimento e 5 mm de diâmetro será usado na fabricação de uma viga de concreto protendido. Observa-se que o cabo sofre um estiramento de 45 mm quando a força P é aplicada. S
Uma haste de aço com 4 m de comprimento não pode ser estirada em mais de 3 mm, e a tensão normal não deve exceder 150 MPa quando a haste é submetida a uma força axial de 10 kN. Sabendo que E = 200G P
Um tubo de alumínio não deve sofrer um estiramento maior que 0,05 in quando submetido a tensão de tração. Sabendo que E = 10,1x10 6 psi e que a tensão normal máxima admissível é de 14 ksi, determine (
Um bloco de 10 in. de comprimento e seção transversal de 1,8x1,6i n deve suportar uma força de compressão centrada P. O material a ser utilizado é um bronze para o qual E = 14x10 6 p s i . Determine a