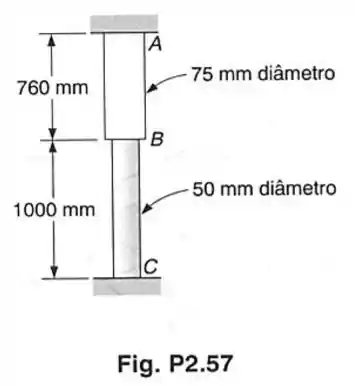
Uma barra composta de duas porções cilíndricas A B e B C é engastada em ambas as extremidades. A porção A B é de latão ( E = 105G P a ; α = 20,9 × 10 - 6 / ° C ) e a porção B C é de aço ( E = 200G P a ; α = 11,7 × 10 - 6 / ° C ). Sabendo-se que a barra está inicialmente sem tensão, determinar: (a) as tensões normais induzidas na porção A B e B C , por uma temperatura aumentada de 30°C; (b) a correspondente deflexão no ponto B .

A) σ A B = 205,85M P a σ B C = 463,15M P a B) δ B = - 1,015m m

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 57

Uma barra composta de duas porções cilíndricas e é engastada em ambas as extremidades. A porção é de latão () e a porção é de aço (). Sabendo-se que a barra está inicialmente sem tensão, determinar: (a) as tensões normais induzidas na porção e , por uma temperatura aumentada de 30°C; (b) a correspondente deflexão no ponto .

Passo 1

Este problema consiste basicamente em somar as deflexões de e e igualar a zero, já que, por estarem engastadas, não haverão variação do comprimento. Mas temos de lembrar que existem também a variação pela dilatação térmica então vamos ter que:

Observe que as dilatações referentes à temperatura são positivas porque estimulam um crescimentod a barra, enquanto às relativas à compressão são negativas porque impedem tal dilatação.