Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 105a
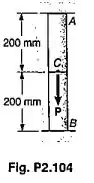
Para a barra composta do Problema 2.104, se P cresce gradualmente desde zero até a deflexão do ponto C atingindo um valor máximo e depois retorna a zero, pede-se determinar o máximo valor de P, a máxima tensão em cada porção da barra e a deflexão permanente em C, quando
Passo 1
Primeiro de tudo, precisamos saber o quanto cada barra aguenta de deformação elástica.
Para isso, vamos usar a Lei de Hooke:
Logo:
E vamos aplicar a Lei de Hooke considerando a tensão de escoamento de cada barra. Assim, vamos descobrir o máximo de deformação elástica que cada barra aguenta.
Também podemos calcular a maior força que cada barra pode resistir para se manter em regime elástico:
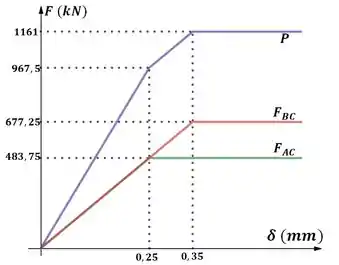
Agora que já calculamos as forças e as deformações podemos gerar o gráfico de Carga-Deformação:
(OBS: Caso tenha dúvidas sobre a construção deste gráfico, veja a questão 104a, onde detalhamos a sua construção)
Passo 2
Note que as duas barras estão acopladas. E como dois corpos não podem ocupar o mesmo lugar ao mesmo tempo, uma barra só pode esticar se a outra encolher. Assim as barras sempre terão a mesma deformação, uma em tração e a outra em compressão:
Como a questão nos dá o valor do alongamento máximo, podemos comparar as deformações calculadas nos passos anteriores.
Como a deformação de tração máxima em AC é maior do que a deformação elástica de tração permitida, então o regime de AC é plástico:
Já no caso da barra BC, a deformação elástica de compressão permitida é maior que a deformação de compressão que de sofrida de fato. Então o regime é elástico.
Passo 3
Agora temos tudo que precisamos para calcular as forças em cada barra!
A região AC está em regime plástico de tração. Então a força que atua sobre ela é igual a força de escoamento:
Já a barra BC está em regime elástico de compressão. Então podemos calcular a força sobre ela utilizando a lei de Hooke e a definição de tensão:
Passo 4
A força externa que causa deformação é a força .
Parte da força gera a tração em e a outra parte gera a compressão em .
Então para calcular a força , basta somar novamente e
Passo 5
Como já calculamos as forças, podemos calcular as tensões em cada porção.
Na porção que está sobre regime plástico, a tensão tem que ser igual a tensão de escoamento:
Já na porção BC podemos usar a equação da tensão:
Passo 6
Para calcular a deformação precisamos do gráfico que construímos:
Repare que a linha tracejada é paralela a primeira porção da linha roxa.
Com isso, vamos determinar a deformação recuperada:
A deformação permanente será: