Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 87

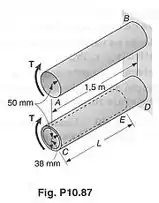
Torques T de mesma intensidade são aplicados aos eixos de aço A B e C D . Usando o método do trabalho e energia, determinar o comprimento L da porção vazada do eixo C D , para que o ângulo de torção em C seja igual a 1,25 vezes o ângulo de torção em A .

Passo 1

Faaala, meus chuchus! Tudo bem? Vamos fazer uma questão de cálculo de ângulo de rotação da torção através do método de energia?

A questão mostra dois eixos A B e C D sendo torcidos pelo mesmo torque T . A única diferença entre os eixos é que o eixo A B é maciço e o eixo C D é vazado. O enunciado quer saber qual o valor do comprimento L da parte vazada de C D que faz o ângulo de rotação na extremidade de C D θ C ser igual a 1,25 vezes o ângulo de rotação na extremidade de A B θ A .

θ C = 1,25 θ A

Podemos calcular θ C a partir da equação que determina a energia U C D que o eixo C D absorve ao se deformar e calcular θ A a partir da equação que determina a energia U A B que o eixo A B absorve ao se deformar.

U C D = T θ C 2       ⟹       θ C = 2 U C D T           |           U A B = T θ A 2       ⟹       θ A = 2 U A B T

Para calcular U A B e U C D usamos a equação 10.22 do livro que calcula a energia absorvida por um eixo em torção.

Mas atenção! O eixo C D tem que ser dividido em duas partes para calcular essa energia! Para ele, calcularemos a energia U C E da parte C E vazada e a energia U E D da parte E D maciça.

U A B = T 2 L A B 2 G J A B

U C D = U C E + U E D       ⟹       U C D = T 2 L 2 G J C E + T 2 L C D - L 2 G J E D

G é o módulo de elasticidade transversal do material das barras. L C D e L A B são os comprimentos totais dos eixos C D e A B . Os dois comprimentos valem 1,5   m . L C D - L é o comprimento da parte vazada do eixo C D . J A B , J E D e J C E são os momentos de inércia polares de A B , E D e C E respectivamente. Vamos calculá-los no próximo passo.

Passo 2

Antes de achar as energias de deformação U A B e U C D de cada barra, temos que encontrar os valores dos momentos de inércia polares J A B , J E D e J C E de cada barra .

Achamos J A B e J C D , através das fórmulas de momentos de inércia polares para áreas circulares abaixo. Antes, devemos converter os draios de m m pra m , multiplicando eles por 10 - 3 .

J A B = π × R A B 4 2       ⟹       J A B = π × 50 × 10 - 3 4 2       ⟹       J A B = 9 , 81747 × 10 - 6   m 4

J E D = π × R E D 4 2       ⟹       J E D = π × 50 × 10 - 3 4 2       ⟹       J E D = 9 , 81747 × 10 - 6   m 4

A fórmula do momento de inércia polar J C E da parte vazada é um pouco diferente dos momentos de inércia polar das partes maciças. Na equação de J C E , temos que levar em conta o raio interno R i da parte vazada que vale 38   m m .

J C E = π × R C D 4 - R i 4 2  

J C E = π × 50 × 10 - 3 4 - 38 × 10 - 3 4 2

  J C E = 6 , 54215 × 10 - 6   m 4

Com esses valores podemos partir para nosso passo final!

Passo 3

Substituímos J A B , J C E e J E D nas equações de U A B e U C D para achar as energias de deformação.

U A B = T 2 L A B 2 G J A B       ⟹       U A B = T 2 × 1,5 2 × G × 9 , 81747 × 10 - 6

U C D = T 2 L 2 G J C E + T 2 L C D - L 2 G J E D       ⟹       U C D = T 2 L 2 G × 6 , 54215 × 10 - 6 + T 2 1,5 - L 2 G × 9 , 81747 × 10 - 6

Substituindo esse valor na fórmula de θ A e θ C , achamos:

θ A = 2 U A B T       ⟹       θ A = 1,5 9 , 81747 × 10 - 6 T G  

θ C = 2 U C D T       ⟹       θ C = 1,5 9 , 81747 × 10 - 6 + 1 6 , 54215 × 10 - 6 - 1 9 , 81747 × 10 - 6 L T G

Colocando esses valores de θ C e θ A na equação que relaciona esses dois ângulos.

θ C = 1,25 θ A

1,5 9 , 81747 × 10 - 6 + 1 6 , 54215 × 10 - 6 - 1 9 , 81747 × 10 - 6 L T G = 1,25 × 1,5 9 , 81747 × 10 - 6 T G

Cortando T G dos dois lados:

1 6 , 54215 × 10 - 6 - 1 9 , 81747 × 10 - 6 L = 0 , 25 × 1,5 9 , 81747 × 10 - 6

L = 0 , 2 50   m

Uhuuul! Terminamos a questão! :-D

Resposta

L = 0 , 2 50   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um colar D de 6k g tem uma velocidade v 0 = 4,5m / s , quando ele se com uma pequena placa presa na extremidade A da barra A B , de diâmetro 20m m . Usando-se E = 200G P a , determinar:a carga estátic
Para a viga prismática mostrada, determinar a declividade no ponto D .
Para a viga prismática mostrada, determinar a deflexão na extremidade A .
Para a viga prismática mostrada, determinar a declividade no ponto D .
Para a viga prismática mostrada, determinar:a declividade na extremidade B ;a deflexão no ponto médio C .