Para a barra composta do Problema 2.106, de P cresce gradualmente desde zero até e depois retorna a zero, pede-se determinar a máxima deformação na barra, a máxima tensão em cada lâmica e, a deformação permanente na barra.
Passo 1
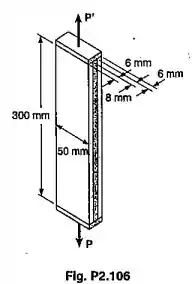
Primeiro, vamos calcular as áreas de seção transversal.

Passo 2
Agora vamos gerar o gráfico Carga-Deflexão para o Aço Doce.
Usando a lei de Hooke vamos determinar a deformação elástica admissível:
E podemos calcular também a carga necessária para atingir o regime plástico:
Com essas informações podemos construir o gráfico de Carga-Deflexão:

Passo 3
Agora vamos gerar o gráfico Carga-Deflexão para o Aço Temperado.
Determinamos a máxima deformação elástica
E a máxima deformação plástica.
Aproveitamos também para calcular a força necessária para deformação a barra em em :

Passo 4
Agora que temos os dois gráficos
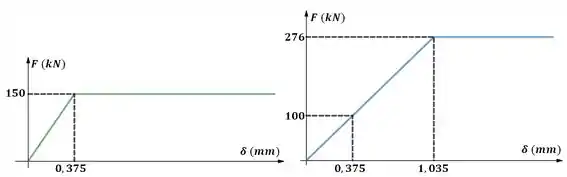
Vamos somar os dois gráficos para obter o gráfico total:
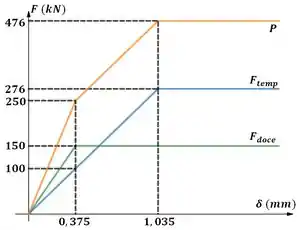
Passo 5
Vamos colocar a força no gráfico.
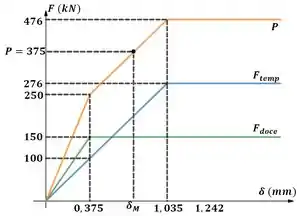
O aço doce está sobre regime plástico, logo a força sobre o aço doce é:
E a força sobre o aço temperado pode ser calculada como:
Passo 6
A máxima tensão no aço doce é igual a tensão de escoamento:
E a tensão no aço temperado pode ser calculada:
Passo 7
A deformação pode ser calculada considerando a deformação elástica do aço temperado aplicando a lei de hooke
Aplicamos a fórmula da tensão:
Reorganizamos:
Aplicamos os valores:
Passo 8
Quando a força for aliviada, a estrutura vai se recuperar seguindo a linha laranja tracejada. Perceba que a linha tracejada é paralela a primeira região da linha laranja contínua.
Usando semelhança de triângulos podemos calcular a deflexão recuperada.
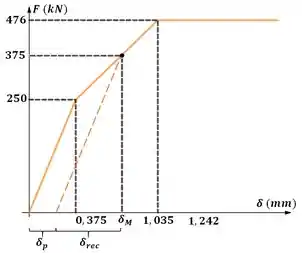
Então a deflexão permanente será: