Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 63
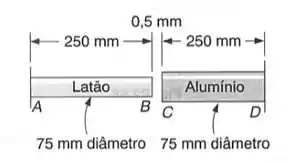
A barra AB é de latão e a barra CD de alumínio (). Sabendo-se que a 16°C a fenda existente entre as extremidades das barras é de , determinar:
- A tensão normal em cada barra, depois que a temperatura for aumentada para ;
- A deformação da barra AB nesse instante.
Passo 1
Sabemos que as barras iram aquecer e deverão vencer os vãos que elas fazem parte, e irão começar a se pressionar, com isso, elas produziram forças que deveremos calcular.
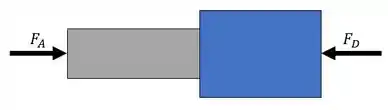
Mas agora precisamos de uma equação de compatibilidade para podermos resolver o nosso problema. Perceba que a deformação total entre os pontos A e D tem que ser igual a distância entre as barras, que nesse caso é 0,5mm no somatório de deformações, e que teremos deformações devido a temperatura e devido aos normais que aparecem nas paredes, dessa forma teremos que:
Em que:
E sabemos que os dados do enunciado são dados por:
E agora só precisamos determinar os normais relacionados com as forças que queremos descobrir.
Passo 2
Usando o nosso diagrama teremos que:
- Trecho AB
- Trecho BC
Sendo assim teremos que:
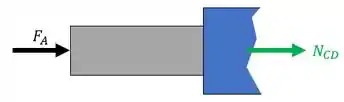
Sendo assim teremos que:
Substituindo na nossa fórmula teremos que:
Passo 3
Se temos a força podemos definir as tensões normais, que é a força dividido pela área da seção, sendo assim teremos que:
- Barra AB e CD terão a mesma tensão por terem a mesma área
E sabemos que para determinar a deformação ada barra AB precisamos fazer o seguinte: