Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 72
A barra de alumínio AD é ajustada a uma camisa, onde é aplicada uma pressão hidrostática de , no trecho BC de comprimento igual a . Sabendo-se que , determinar:
- A variação do comprimento total AD da barra;
- A variação do diâmetro no ponto médio da barra.
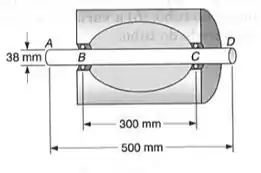
Passo 1
Perceba que no trecho BC a pressurização afeta todo o entorno da barra, ou seja, tanto na direção x (para dentro da folha) quando na direção z (vertical) temos tensões agindo como compressão no tubo BC. Já na direção y (horizontal) não temos ação de força nem de tensão nenhuma, por isso podemos fazer a seguinte suposição:
E perceba que usamos negativo por se tratar de uma pressão negativa (ou seja, de compressão).
Sabemos pelo enunciado também que:
Passo 2
Agora vamos definir as deformações da nossa barra pela fórmula:
Substituindo os valores vamos ter que:
Passo 3
Agora definindo as deformações pedidas, podemos ver o seguinte:
- O enunciado pede a deformação em AD
- O enunciado pede a deformação do diâmetro que é D=38mm.
Perceba que a deformação em AD só será modificada no trecho BC, ou seja, o trecho BC irá definira deformação, e por isso teremos que:
E a fórmula é dada por:
E assim temos a deformação total no trecho AD.
O diâmetro da barra é dado por: