Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 15

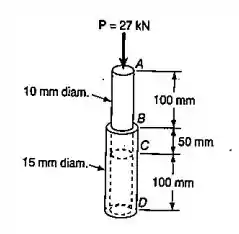
Uma barra maciça de latão de 150   m m de comprimento e 10   m m de diâmetro se ajusta perfeitamente, dentro de um tubo de mesmo comprimento, com 15   m m de diâmetro externo e 10   m m de diâmetro interno. Uma porção de 50   m m   da barra está colada ao tubo e sobre esta é aplicada uma carga de 27   k N , como mostrado. Sabendo-se que E = 105   m m , determinar: ( a ) a deflexão do ponto A ; ( b ) o máximo valor de tensão normal nesse conjunto.

Passo 1

Fala aí galera, bora fazer mais uma questão de Resmat. Primeiramente, vamos encontrar a área da barra interna.

A i n t = π 4 d 2 = π 4 0,010 2

A i n t = 7,85 × 10 - 5   m 2

Já para a barra de externa, temos:

A e x t = π 4 d 2 = π 4 0,015 2

A e x t = 1,767 × 10 - 4   m 2

Com isso, podemos encontrar a deformação para cada barra, fica assim:

δ A B = F A B L A B E A A B = 27000 ( 0,1 50 ) ( 105 × 10 9 ) ( 7,85 × 10 - 5 )

δ A B = 4,91.10 - 4   m

E para a barra externa, temos:

δ B C = P B C L B C E B C A B C = 27000 0 , 1 50 105 × 10 9 1,767 × 10 - 4

δ B C = 2,18.10 - 4   m

Então a deflexão do ponto A é igual a soma das duas deformações:

δ A = 4,91.10 - 4 + 2,18.10 - 4

δ A = 0,709   m m

Passo 2

Para determinarmos o máximo valor da tensão normal é só pegar a força e dividir pela menor área:

σ = F A

σ = 27000 N 7,85 × 10 - 5   m 2

σ = 343,95   M P a

Resposta

δ A = 0,709   m m

σ = 343,95   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de latão de 300m m de comprimento, com 30m m de diâmetro externo e 3m m de espessura, é fixado em um torno mecânico manual, que está ajustado de tal modo que os mordentes encostem nas suas ext
10.43 O bloco cilíndrico E de 18 lb tem uma velocidade horizontal v 0 quando atinge diretamente o batente BD que está conectado às hastes AB e CD com diâmetro de 1 8 ¯ = i n . Sabendo que as hastes sã
Duas barras cilíndricas, uma de aço ( E = 200G P a ) e outra de latão ( E = 105G P a ), são ligadas em C e engastadas em A e E . Para o carregamento indicado, determinar: (a) as reações em A e E ; (b)
Um tubo de latão de 300m m de comprimento, com 30m m de diâmetro externo e 3m m de espessura, é fixado em um torno mecânico manual, que está ajustado de tal modo que os mordentes encostem nas suas ext
Duas barras cilíndricas, uma feita de aço ( E = 200G P a ) e a outra de latão ( E = 105G P a ), são ligadas em C . A barra composta é engastada em A , enquanto que existe uma folga de 0,12m m entre a