Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 29

Determinar a deflexão do cume A de um cone circular homogêneo, de altura h , densidade ρ   e módulo de elasticidade E ,   devido ao seu próprio peso.

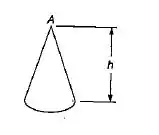
Passo 1

Fala aí galera, partiu mais uma questão de Resmat. Primeiramente, sabemos que a deflexão é dada por:

δ = - P L A E

Sabemos que o volume do cone é dado por:

V = π r 2 h 3

Já a área do cone é dada por:

A = π R 2 + π r g '

Onde g '   é a geratriz.

Portanto, sabemos que:

P = m g = ρ V g = ρ π r 2 h 3 g

L = h

A = π R 2 + π r g '

Portanto, a deformação será:

δ = - π r 2 h 2 ρ g 3 π R 2 + π r g ' E = - r 2 h 2 ρ g 3 R 2 + r g ' E

Resposta

δ = - r 2 h 2 ρ g 3 R 2 + r g ' E

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo-se que a haste de ligação BD tem uma seção transversal uniforme, de área igual a 800m m ² ², determine a intensidade da carga P para que a tensão normal na haste BD seja 50M P a .
Cada uma das hastes de ligação AB e CD tem uma seção transversal retangular uniforme de 6,3 × 25,4m m e está ligada à barra horizontal BCE por pinos de diâmetro igual a 25,4m m . Considerando que a te
Cada uma das quatro hastes verticais, ligadas às duas barras horizontais, tem uma seção transversal uniforme de 10 × 40m m e os pinos tem diâmetro de 14 mm. Determine o máximo valor da tensão normal m
Duas cargas verticais são aplicadas ao pino B da montagem indicada. Sabendo-se que o diâmentro do pino usado em cada ligação é de 15,2m m , determine o valor máximo da tensão normalmédia na (a) haste
Determine a menor área admissível para a seção transversal da barra D E da treliça mostrada, se para o carregamento dado, a tensão normal nesta barra não deve ultrapassar 138M P a .