Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 74

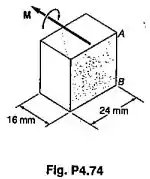
Uma barra prismática AB é feita de um aço que considerado ser elastoplásticos com E =200 GPa e σ e = 250   M P a . Sabendo-se que M = 450   N m , determinar (a) a espessura do núcleo elático (b) o raio de curvatura da barra

s

Passo 1

Vamos começar a questão calculando as propriedades geométricas.

I = 1 12 b h = 1 12 ⋅ 16 ⋅ 24 3 = 18432   m m 4

c = h 2 = 24 2 = 12   m m

Passo 2

Vamos usar a equação 4.33 para determinar o maior momento elástico admissível:

M e = I c σ e = 18423   m m 4 12   m m ⋅ 250   M P a = 384   N ⋅ m

O momento calculado é menor do que o momento que é aplicado na viga; Isso quer dizer que o regime é elastoplásticos.

Passo 3

Agora que já sabemos que o regime é elastoplásticos, vamos calcular o núcleo elástico. Para isso vamos usar a equação 4.38:

M = 3 2 M e 1 - 1 3 y e 2 c 2  

Isolamos o y e :

y e = 3 c 2 1 - 2 3 ⋅ M M e

y e = 3 ⋅ ( 12   m m ) 2 1 - 2 3 ⋅ 450   N ⋅ m 384   N ⋅ m

Logo:

y e = 9,72   m m

A espessura é:

E s p e s s u r a = 2 y e = 19,44   m m

Passo 4

Para calcular o raio de curvatura em regime elastoplásticos usamos a equação:

ρ = y e E σ e = 9,72   m m ⋅ 200   G P a 250   M P a = 7776   m m

ρ = 7,776   m

Resposta

E s p e s s u r a = 2 y e = 19,44   m m

ρ = 7,776   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

sabendo-se que uma viga de seção transversal mostrada é encurvada sobre um eixo horizontal, e que está submetida a um momento fletor de 4 k N m , determinar a intensidade total da força que atua na po
Resolver o P r o b4.14 , considerando que a viga é encurvada em torno de um eixo vertical por um momento de 4k N m .
Para o perfil mostrado, determinar o maior momento M que pode ser aplicado, sem que as seguintes tensões admissíveis sejam excedidas: σ a d m = + 40M P a e : σ a d m = - 100M P a .
Um momento de 3,5k N m é aplicado à barra de aço mostrada. Pede-de:Sendo que o momento encurva a barra em torno do eixo horizontal, determinar a máxima tensão e o raio de curvatura;Resolver a parte a)
Sabendo-se que, para a viga extrudada mostrada na figura, a tensão admissível é de 120M P a , à tração, e 15 0M P a à compressão. Determinar o maior momento M que pode ser aplicado.