Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 72
A barra prismática é feita de um aço que é considerado ser elastoplásticos com E=200GPa e . Para um momento de 150 Nm, paralelo ao eixo z e aplicado na extremidade B, como mostrado, determinar (a) a espessura do núcleo elástico; (b) o raio de curvatura da barra.
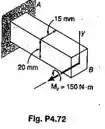
Passo 1
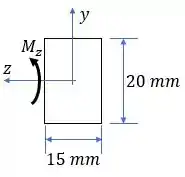
Vamos começar a questão calculando as propriedades geométricas da viga
Passo 2
Agora podemos calcular a tensão máxima:
Observe que a máxima tensão sobre a viga é menor doque a a tensão de escoamento. Isso quer dizer que não há região plástica na viga. Ou seja, a espessura do núcleo elástico é igual a espessura da viga:
Passo 3
Agora é só calcular o raio de curvatura:
E prontinho! Finalizamos a questão
Resposta
Exercícios de Livros Relacionados
Para o perfil mostrado, determinar o maior momento M que pode ser aplicado, sem que as seguintes tensões admissíveis sejam excedidas: σ a d m = + 40M P a e σ a d m = - 100M P a .
Sabendo-se que, para a viga extrudada mostrada na figura, a tensão admissível é de 120M P a , à tração, e 15 0M P a à compressão. Determinar o maior momento M que pode ser aplicado.
Uma tira de aço de 900 m m de comprimento é encurvada, formando uma circunferência completa, por dois momentos aplicados como mostrado. Determinar:A máxima espessura t da tira, se a tensão admissível
Uma lâmina de aço, que originalmente estava reta, é montada sobre uma serra de fita, que passa sobre polias de 200m m de diâmetro. Determinar a máxima tensão na lâmina, sabendo-se que ela tem uma espe
Barras retas de 6 mm de diâmetro e 30 cm de comprimento são enroladas e armazenadas dentro de um tambor de 1,25m de diâmetro interno. Considerando que a resistência ao escoamento não deve ser excedida