Uma barra retangular é feita de um material para o qual o modulo de elasticidade é em tração e em compressão. Mostre que a curvatura da barra em flexão pura é

Em que:

Para essa questão vamos precisar usar o mesmo conceito que já usamos no caso de concreto e aço, mas no nosso caso, vamos usar o modulo de elasticidade a tração como a nossa referência.

Vamos então transformar o trecho em compressão e vamos manter intacto o trecho em tração, assim vamos ter que:

E o que fazíamos com esse fator? Multiplicávamos ele pela largura da nossa seção, certo? Aqui vamos usar um conceito parecido, porém, não igual, porque vamos ter que multiplicar pela área da seção em compressão, assim vamos ter que a nossa seção é dada por:

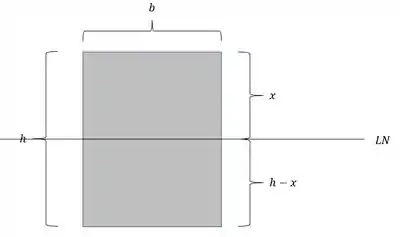
Perceba que ainda não temos a LN, mas como sabemos que ela separa a região em compressão da região em tração, definimos ela em uma posição .

Mas pensa no seguinte, a nossa seção é dada por:

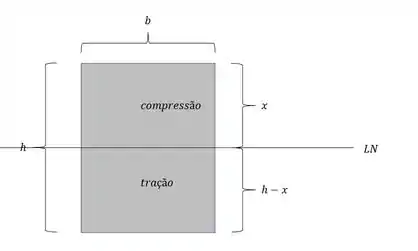
E a LN? É bem simples é só fazer a área de compressão transformada multiplicando pela distância do centroide dela até a suposta LN, e isso tem que ser igual a área de tração multiplicada pela distância dela até a suposta LN, assim temos que:

OBS: á área de compressão modificada é só pegar a área dela e multiplicar pelo fator que determinamos lá em cima, assim temos que:

E podemos aproveitar para fazermos a seguinte relação:

Multiplicando tudo por -1 teremos que:

Para o momento de inércia, temos a seguinte equação a ser feita:

E porque temos esse temos esse termo de área na equação? PORQUE ESSA ÁREA É A ÁREA MODIFICADA, OU SEJA, TEM QUE TER OBRIGATORIAMENTE O FATOR DE CONVERSÃO, ENTÃO NÃO PODEMOS ESQUECER DE MANEIRA NENHUMA.

e para a tração teremos que:

Assim teremos que:

E já sabemos que:

Substituindo temos que: