Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 53

Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar também o máximo valor absoluto,

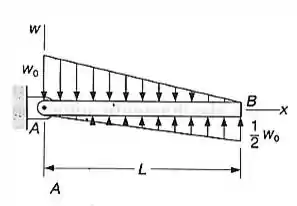
Passo 1

E ai gurizada tudo beleza? Espero que sim!!

A carga triangular em qualquer ponto x da viga é calculada a partir dessa equação:

w   x = W o   ×     1 - x L - W o 3 × x l

Logo teremos a seguinte simplificação:

w   x = W o   ×     1 - 3 x L

Passo 2

Nós temos a seguinte definição: Vb-Vc= - ∫ x L w x d x

= 0 - V x = - ∫ x L w x d x

V x = ∫ x L w o ×     1 - 3 x L d x

Galera e para resolver essa integral vem comigo, vamos substituir os limites de integração...

V x = W o L - 3 L 2 2 L + x - 3 x ² 2 L

V x = W o / 2 L L ² - 3 x ² + 2 x L

Passo 3

Para acharmos o momento fletor máximo precisamos encontrar o ponto onde a cortante é igual a zero, então vamos dizer que V=0

V x = W o / 2 L L ² - 3 x ² + 2 x L

L ² - 3 x ² + 2 x L = 0

Podemos fazer a seguinte analogia:

x L = 1 3

x = L 3

Passo 4

O momento fletor é a integral da equação da força cortante, então..

d M d x = V

M B - M c = ∫ x L V   X d x

M x = ∫ x L w o 2 L ×     L ² - 3 x ² + 2 x L d x

Calculando os limites de integração temos:

M x = w o 2 L × L 3 3 - x 3 + x ² L

Agora devemos substituir os limites de integração

M x = w o 2 L × L 4 3 - L + L 3 - L 3 3 - x 3 + x ² L

Passo 5

Para calcularmos então o momento máximo fletor , teremos que substituir a analogia do passo 3: x = L 3

M x = w o 2 L × L 4 3 - L + L 3 - L 3 3 - x 3 + x ² L

Substituindo temos:

M x = w o 2 L × L 4 3 - L + L 3 - L 3 3 - ( L 3 ) ³ + ( L 3 ) ² L

M x = w o 2 L × L 4 3 - L + L 3 - L 3 3 - ( L 3 27 ) + L 3 9

M x = w o 2 L × L 4 3 - L + ( 20 L 3 27 )

M x = w o 2 L × L 4 3 - L + ( 20 L 3 27 )

M x = W o × L 3 3 - 1 2 + 10 L 2 27

Resposta

  1. V x = W o / 2 L L ² - 3 x ² + 2 x L e   M x = w o 2 L × L 4 3 - L + L 3 - L 3 3 - x 3 + x ² L

b )   x = L 3 e M x = W o × L 3 3 - 1 2 + 10 L 2 27

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga ABC sob o carregamento mostrado. (b) Use a equação obtida para M para determinar o momento
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine o valor máximo do momento fletor na viga.
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine o valor máximo do momento fletor na viga.
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine o valor máximo do momento fletor na viga.
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo momento fl