Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 87

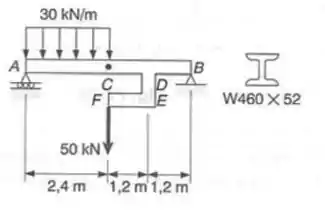
A barra rígida DEF é soldada ao ponto D da viga constituída de um perfil laminado de aço AB. Para o carregamento mostrado, determinar a) a declividade em A b) a deflexão do ponto médio C da viga. Usar E= 200 GPa

Passo 1

E ai gurizada tudo belezinha??? Vamos analisar a viga em questão... antes de tudo vamos desenhar o diagrama de corpo livre :D

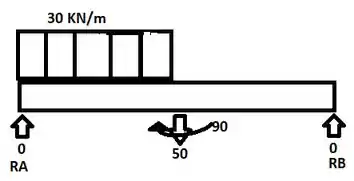
Primeiramente vamos calcular o somatório de momentos, venha comigo?

+ ↺ ∑ M a = F   x   d = 0

- 4,8   R a + 30 × 2,4 × 1,2 + 50 × 1,2 = 0

R a = 3   K N

Agora teremos que montar a função para posteriormente integrarmos ....

E I d 2 y d x 2 = M = - 25 3   x - 1,2 3 + 45   x - 1,2 ² - 1 6 30 × x - 1,2 ³ + c 1

Integrando teremos....

Integrando mais uma vez teremos....

E I y = - 25 3   x - 1,2 3 + 45   x - 1,2 ² - 1 24 30 × x - 1,2 4 + C 1 x + C 2

Considerando que o comprimento da viga é L 4,8 m ou seja, x=4,8 então substituiremos na equação acima e teremos....

0 = - 25 3   4,8 - 1,2 3 + 45   4,8 - 1,2 ² - 1 24 30 × 4,8 - 1,2 4 + 4,8 C 1

0 = - 1944 5 + 2916 5 - 210 + 4,8 C 1

C 1 = 3,25   K N m ²

Passo 2

Analisando o perfil dado pelo exercício podemos buscar os valores do perfil no anexo ao livro para encontrarmos o valor da inércia, que é: 202 x 106 mm4 = 202 x 10-6 m4

E I = 200 × 10 9 × 20 2 × 10 - 6 = 40,4 × 10 6 N m ²

Passo 3

Agora para encontrarmos a deflexão vamos considerar que: x= 0

∅ = 3,25 40,4 × 10 6 = 8,04 × 10 - 8 r a d

Passo 4

Agora para encontrarmos a deflexão vamos considerar que: x= 1,2

E I y = C 1 × 1,2 = 3,25 × 1,2 = 3,9   K N m ³

Y = 3,9 40,4 × 10 6 = 9,65 × 10 - 8 m

Resposta

  1. 8,04 × 10 - 8 r a d
  2. 9,65 × 10 - 8 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrados na figura, determine ( a ) a equação da linha elástica para a parte A B da viga, ( b ) a deflexão no meio do vão e ( c ) a inclinação em B .
Sabendo que a viga A B é um perfil de aço laminado W 10 × 33 e que w 0 = 3k N / m , L = 12m m e E = 200G P a , determine ( a ) a inclinação em A e ( b ) a deflexão em C .
Para a viga em balanço e o carregamento mostrados nas figuras, determine ( a ) a equação da linha elástica para a parte A B da viga, ( b ) a deflexão em B e ( c ) a inclinação em B .
Determine a reação no apoio móvel e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados nas figuras.
Para a viga e o carregamento mostrados, determine a reação no apoio móvel quando w 0 = 15k N / m .