Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 163
Resolver o Prob. 162, assumindo que é absorvido em cada engrenagem.
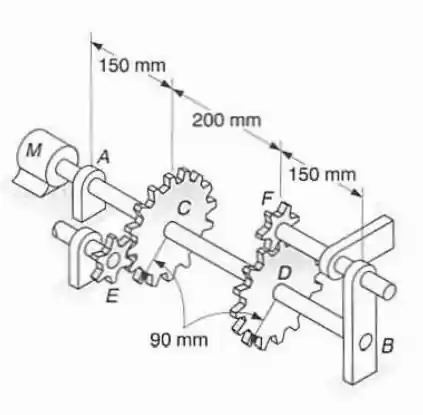
Passo 1
Fala aí, pessoal!! O problema pede o menor diâmetro que o eixo pode ter, para suportar as tensões cisalhantes exercicidas sobre ele.
Para descobrir esse diâmetro a gente utiliza uma equaçãozinha que relaciona os seguintes termos:
Onde é o momento polar de inércia, é o raio, o momento fletor e a torção, além disso temos também a máxima tensão de cisalhamento admissível .
Então percebam que nós temos de encontrar os momentos fletores atuantes no eixo assim como o torque (ou torção) exercido. O problema vai ser resumir basicamente nisso =D.
Então partiu?
Passo 2
Para achar os momentos fletores e as torções vamos fazer um diagrama de forças aplicadas ao eixo:
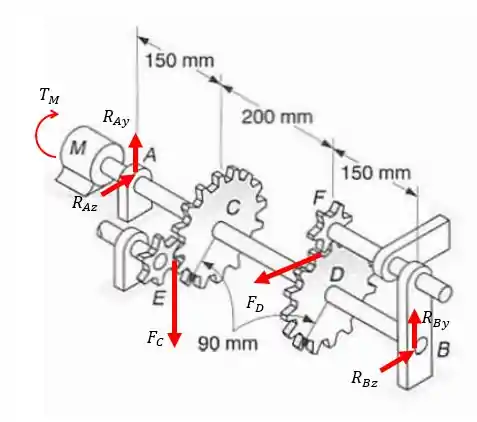
Agora vamos achar o torque. Vejam que o problema nos fornece uma rotação e uma potência , vamos utilizar esses dados para calcular o torque. Vamos fazer isso dividindo a potência transmitida pela velocidade angular:
E vamos calcular a frequência:
Então o torque que cada engranagem está submetida, de forma a absorver a potência de deve ser igual a:
Pessoal, além disso a gente tem que assumir que as engrenagens e , por estarem em contato com as engrenagens e , respectivamente, vão possuir o mesmo torque!! Dessa forma:
Passo 3
Galera, se a gente achou os torques podes facilmente achar as forças. Se lembra que:
Então vamos ter:
Como a engrenagem possui o mesmo raio e está submetida ao mesmo torque então terá a mesma força:
Show de bola, achamos essas duas forças!! Agora a gente pode substituir elas num novo diagrama da seguinte forma:
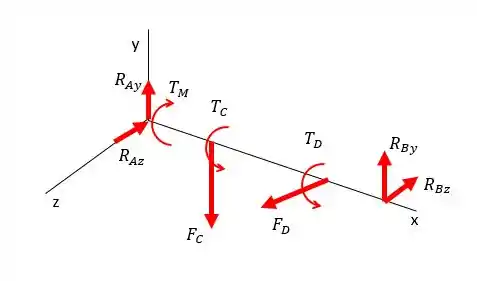
Ih, caraca!!! Agora ficou bem mais tranquilo de ver o problema né? Repara como a gente colocou as forças e atuando diretamente sobre o eixo, a gente pode deslocar essa força (que antes atuava no dente da engrenagem) para o eixo porque aplicamos também o respectivo torque da força!!!
Passo 4
Então a gente já tem os torques falta achar os momentos!!! Mas antes a gente precisa descobrir ainda quais são as forças atuantes em e em . Que tal substituir os valores que já calculamos no diagrama acima?
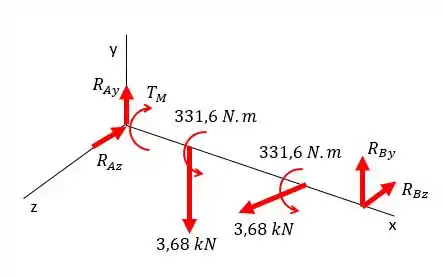
Show of pelotas!!
Agora a gente acha as forças restantes com as equações da estática:
Para as forças em :
Para as forças em :
Para os momentos em :
Para os momentos em :
Com esses valores a gente pode achar as resultantes em também:
Só pra ficar organizadinho:
Passo 5
Parece que essa questão não acaba nunca né pelo amor.....
Mas já ta acabando eu juro!! Agora a gente só vai achar os bentidos momentos fletores. Para isso vamos olhar novamente nosso diagrama com os valores atualizados:
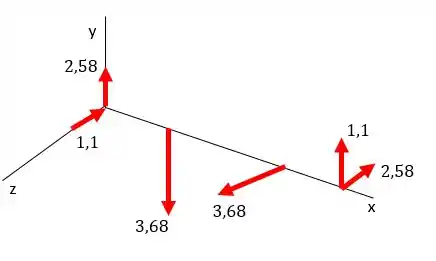
O que aconteceu com as torções?
Ficaram de fora porque não influenciam o momento fletor!
Agora vamos calcular o momento fletor nos pontos e que são os pontos críticos do problema:
Para :
Para :
Ufaaaa!!! Estamos prontos para o último passo galeraaaa!!!!
Passo 6
Agora a gente finalmente vai utilizar a nossa equação:
Perceba que temos momento em duas direções então vamos ter:
Beleza, agora qual ponto utilizar? O ponto ou ? A gente vai utilizar os dois e ver qual tem o termo mais elevado. Mas nesse caso específico os valores dos momentos são iguais, são estão trocados. Então o que vai influenciar mais será o valor da torção. Vamos calcular a torção para cada termo:
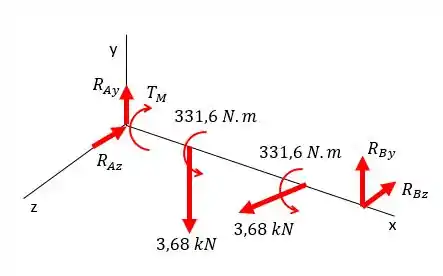
Analisando a figura a gente pode ver que o torque realizado pelo motor é igual à soma dos torques das engrenagens:
Dessa forma o local onde se encontra o maior torque é na seção do eixo. Como os momentos em e são iguais mas o torque de é maior então vamos utilizar o ponto :
Só para observar que nesse ponto o torque é igual ao torque do motor .
obs: Galera na real o ponto não será o ponto crítico o ponto crítico é o imediatamente antes ao ponto . Mas isso não faz muito diferença agora, embora seja legal saber disso =D
Agora vamos achar o termo :
Assim:
Substituindo: