Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 2
A barra uniforme AO tem um peso de 50 N. Quando a barra está na posição vertical, θ=0º, a mola está livre. Determine o ângulo θ para o equilíbrio se a extremidade da mola contorna a periferia do disco enquanto o disco gira
Passo 1
Fala ai galerinha bonita, tudo beleza?
Saca só, o enunciado nos deu um barra uniforme de peso atuando em um sistema de molas como no diagrama abaixo:
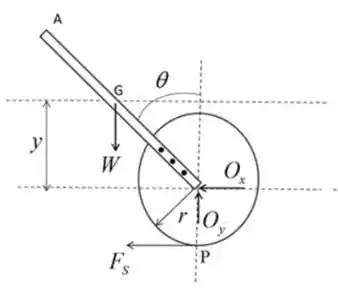
Onde é a força peso da barra e é a força que a mola exerce. Além disso temos as reações de apoio e . E sabendo que em a mola está está relaxada, o enunciado pede pra gente determinar os valores de que deixam o sistema em equilíbrio.
Iradoso, pra isso vamos usar as malandragens do trabalho virtual pra nos ajudar.
Passo 2
Como e são forças de reações de apoio, elas não são consideradas no cálculo do trabalho virtual, iremos usar apenas a força peso e a força elástica da mola.
Show de bolinhas, começando pela força elástica, temos sua equação:
Onde é a constante elástica e a deformação da mola. Como o enunciado nos diz que a mola contorna a periferia do disco, quer dizer que a deformação da mola vai ser do tamanho desse arco que contornou o disco de raio de .
Então a força será dada como:
Dado que e , vamos obter:
Maravilha, e como o deslocamento é dado , o deslocamento virtual será:
Passo 3
Belezoca, agora a força peso do membro , , atua na posição dada como:
Logo, o deslocamento virtual será:
Sendo assim, teremos que a soma dos trabalhos virtuais será:
Tal que:
E como essa equação não tem como a gente resolver na mão, podemos ir por tentativa e erro, ou jogar em alguma calculadora hehe
Jogando na calculadora, vamos obter (em radianos):
Mas como queremos apenas ângulos positivos, então teremos:
Passando para graus, vamos descobrir que: