Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 1

A caixa de 200   k g está no elevador pantográfico na posição θ = 30 ° . Determine a força no cilindro hidráulico A D para equilíbrio. Despreze a massa dos componentes da plataforma elevatória.

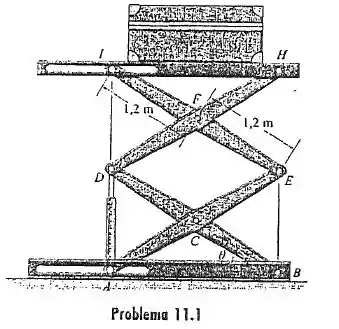
Passo 1

Vamos lá pessoal!

Seguinte, para determinarmos à força aplicada no nosso cilindro, vamos usar o trabalho virtual, mas antes vamos lembrar algumas coisas:

Este cilindro executa uma força para manter a caixa parada, logo, temos que a variação de trabalho é igual a zero. Pois, o sistema está parado.

δ U = 0

Aí a gente vai calcular o trabalho realizado pelas forças ativas desse sistema, P e a força no cilindro que vamos chamar de F A D , calcular a variação de trabalho e igualar a zero.

Com isto em mente, sobrou apenas um probleminha de trigonometria.

Passo 2

Desenhando o diagrama de corpo livre, com os descolamentos virtuais:

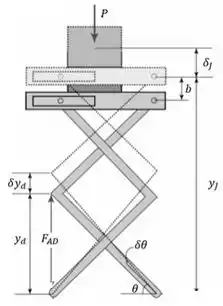
P empurra o sistema para baixo. E o cilindro faz o contrário.

Perceba que y d é deslocamento de F A D , e temos que y J é o deslocamento do nosso peso da caixa.

Para determinarmos o trabalho virtual, temos que determinar o deslocamento causado por cada força.

Vamos determinar o deslocamento de d :

O deslocamento de D é a derivada de y d e vamos encontrar y d por meio deste triangulo retângulo:

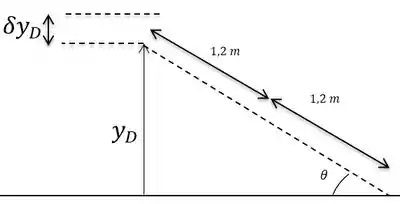
Aplicando s e n o , no triângulo retângulo temos:

s e n   θ = y D 1,2 + 1,2

Isolando y D :

y D = 2,4 ∙ s e n   θ

Derivando dos dois lados de y D teremos nosso deslocamento:

δ y D δ θ = 2,4 ⋅ cos ⁡ θ   δ θ

δ y D = 2,4 ∙ cos ⁡ θ   δ θ

Aí o trabalho causado por F A D é:

F A D ⋅ δ y D = F A D   2,4 ∙ cos ⁡ θ   δ θ

Passo 3

Temos que determinar o deslocamento de y J , vamos seguir o mesmo raciocínio do passo 2. Utilizando o diagrama de corpo livre e pela figura do enunciado, vemos que y d é a metade do comprimento necessário para chegarmos a base da caixa:

Portanto, para o comprimento necessário para y J será o dobro de y D mais o nosso b :

y J = 2 ∙ y D + b

Substituindo y D :

y J = 2 ∙ 2,4 ∙ s e n   θ + b

Derivando y J teremos o seu deslocamento:

δ y j δ θ = 4,8 cos ⁡ θ

δ y J = 4,8 cos ⁡ θ δ θ

Aí o trabalho causado por P é:

P ⋅ δ y j = P   4,8 cos ⁡ θ δ θ

Passo 4

Como já calculamos os deslocamentos, podemos determinar força F A D , por meio da variação do trabalho virtual:

Considerando o vetor força de baixo para cima como positivo e a gravidade como g = 9,81   m / s 2 , temos:

δ U = 0

U F C D - U P = 0

F A D ∙ δ y D - P ∙ δ y J = 0

Substituindo os cálculos:

F A D ∙ 2,4 ∙ cos ⁡ θ   δ θ - ( 200 ∙ 9,81 ) ∙ 4,8 cos ⁡ θ δ θ = 0

Isolando F A D , teremos nossa reposta:

F A D = 200 ∙ 9,81 ∙ 4,8 cos ⁡ θ δ θ 2,4 ∙ cos ⁡ θ   δ θ

Simplificando cos ⁡ θ δ θ , fica:

F A D = 200 ∙ 9,81 ∙ 4,8 2,4 = 3,924   k N

Resposta

F A D = 3,924   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

104- Os colares A e B são conectados por um arame A B e podem deslizar livremente nas barras sem atrito como mostra a figura. Sabendo que o comprimento do arame é 440m m e que o peso W do colar A é 90
O colar B pode deslizar ao longo da barra AC e é fixado por um pino a um bloco que pode deslizar na fenda vertical como mostrado na figura. Deduza uma expressão da intensidade do binário M, necessário
Duas barras idênticas ABC e DBE são conectadas por um pino em B e por uma mola CE. Sabendo que a mola tem comprimento de 4i n quando indeformada e a constante da mola é 8l b / i n , determine a distan
Resolva o problema 10.108 considerando que a carga de 24l b é aplicada em C ao invés de E.
Uma força horizontal P de intensidade de 180 N é aplicada ao mecanismo em C. A constante da mola é k = 1,6k N / m e a mola está indeformada quando θ = 0 . Desprezando o peso do mecanismo, determine o