Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 106
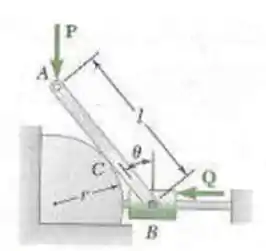
Uma haste delgada de comprimento é presa a um colar em B e repousa sobre uma parte de cilindro circular de raio . Desprezando o efeito do atrito, determine o valor de correspondente a posição de equilibrio do mecanismo quando , , e .
Passo 1
Primeiro, vamos usar a geometria do problema pra definir alguns parâmetros para o trabalho virtual.
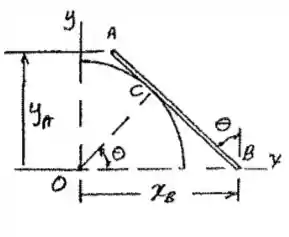
Outro parametro a se definir é o .
Passo 2
Agora temos que aplicar o conceito do trabalho virtual para achar o valor do ângulo para o sistema!
Logo, para os valores descritos la em cima,
Portanto,
Resposta
Exercícios de Livros Relacionados
Substitua o binário M do Prob. 7/6 pela força horizontal P . Como mostrado, e determine o ângulo de equilíbrio θ .
11- A garra superior D da prensa desliza sem atrito ao longo da coluna vertical fixa. Determine a força F necessária sobre a manopla, para produzir uma compressão R sobre o rolamento para qualquer val
29- A elevação da carga de massa m é controlada pelo parafuso de ajuste que une as juntas A e B . A variação da distância entre A e B para uma revolução do parafuso é igual ao passo L do parafuso (ava
27- O projeto existente de um carrinho para colocação de carga em aviões está sob revisão. A plataforma A D do carrinho é elevada até a altura adequada pelo mecanismo mostrado. Existem dois sistemas d
70- Duas cascas semicilíndricas com retângulos projetados iguais são formadas de lâminas metálicas, uma com a configuração a ) e a outra com configuração b ) . Ambas as cascas repousam sobre uma super