Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 23
Uma barra-reboque para avião é posicionada por meio de um cilindro hidráulico, ligado a uma barra cilíndrica de aço com 25mm de diâmetro, que aciona dois braços DEF idênticos, com rodas. O peso total da barra-reboque é de 2KN, e seu centro de gravidade está localizado em G. Para a posição mostrada, determine a tensão normal nessa barra cilíndrica.
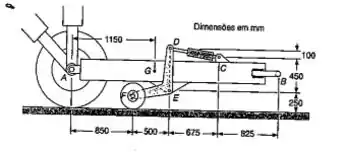
Passo 1
Vamos olhar pro sistema e definir onde estão as forças que interessam pra gente.
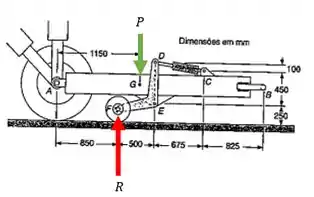
Encare o esforço no ponto C, como um esforço interno e bora fazer o somatório dos momentos em A, para encontrarmos essa reação.
Passo 2
Agora que a gente já tem a reação, vamos analisar os braços DEF.
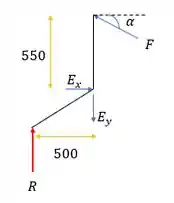
Fazendo o somatório dos momentos no ponto E, a gente vai achar a força F que nos interessa, porém a gente precisa decompor ela na horizontal antes.
Para encontrar o cosseno a gente faz:
Fazendo enfim o somatório dos momentos em E, para eliminar as incógnitas de E, considerando o sentido horário positivo:
Passo 3
Agora é só calcular a área pra gente encontrar a tensão:
E a tensão: