Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 103
A barra ABC consiste em duas porções cilíndricas AB e BC; ela é feita de um aço doce, que é assumido ser elastoplástico com e . Uma força é aplicada à barra até que sua extremida se mova para baixo, de um valor igual a . Determinar o máximo valor da força P e a deformação permanente na barra depois da força ser removida.
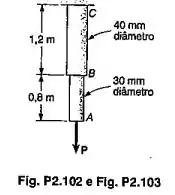
Passo 1
Vamos começar a questão calculando as áreas de seção transversal:
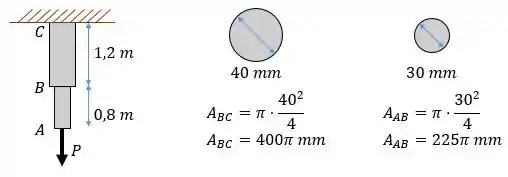
Passo 2
Repare que a estrutura contém duas seções com área de seção transversal diferentes.
A seção AB é menor que a seção BC, isso quer dizer que a seção AB irá entrar em regime plástico com uma força menor do que a necessária para BC.
Contudo, nós queremos evitar a ruptura da estrutura. Então vamos considerar que apenas a região de menor seção entra em regime plástico.
Vamos calcular a força baseados na região de menor seção:
Passo 3
Agora que temos a força, podemos calcular a deformação elástica em cada uma das regiões:
Para a região AB:
Para a seção BC:
A deformação elástica total é:
Passo 4
A questão já nos dá o valor da deformação máxima, vamos usar isso para calcular a deformação permanente: