Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 47
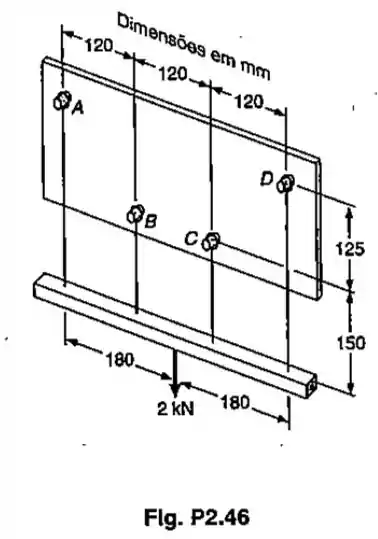
Uma barra rígida é suspensa por meio de quatro arames, fixados a uma placa fina, como indicado. Os arames amarrados aos pinos e são de alumínio () e têm diâmetro de ; enquanto que os demais são de aço () e têm diâmetro de . Sabendo-se que todos os arames estão inicialmente esticados, determinar: (a) a tração adicional em cada arame quando uma carga de é aplicada no ponto médio da barra; (b) o correspondente alongamento dos arames.
Passo 1
O problema pede a tração e a deflexão em cada arame. Ou seja, vamos ter que utilizar, tanto uma equação de forças, no caso o equilíbrio das forças na vertical e do momento, quanto a equação da deflexão.
É importante notar que neste caso a deflexão dos arames e são iguais, assim como as dos arames e . Isso acontece porque a força é aplicada exatamente no meio da barra, mantendo assim uma simetria.
Além disso, por causa da simetria, a deformação de todos os arames serão exatamente iguais!
Passo 2
Vamos fazer o diagrama de corpo livre da barra.
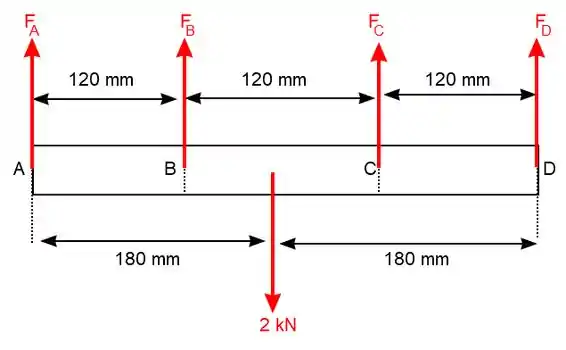
Agora vamos aplicar as equações de equilíbrio:
Passo 3
A deflexão que vamos utilizar, neste caso, será dos fios, da seguinte forma:
Lembrando que:
Vamos substituir os comprimentos, áreas e coeficientes de elasticidade, onde:
Para as áreas de e
Para e
Assim, para
Para
Para
Para
Resumindo
Lembrando que:
Passo 4
Olha só! Se as deformações e então podemos observar que e . Isso já até poderia ter sido percebido antes por causa da geometria.
Então podemos substituir na nossa equação das forças
Ou, simplificando
Além disso, sabemos também que
Logo
Assim
Substituindo na equação anterior
Como
Assim:
Passo 5
Para saber a deflexão de cada fio precisamos achar de um único, pois são todos iguais, portanto:
Resposta
a)
b)