Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 60
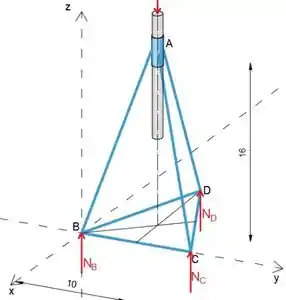
A base de um macaco de automóvel forma um triângulo equilátero de comprimento lateral de 10 pol. E é centralizado sob o colar A. Modele a estrutura como uma com uma esfera e encaixe em cada junta e determine as forças nos membros BC, BD e CD. Despreze quaisquer componentes de reação horizontais sob os pés B, C e D.
Passo 1
Podemos determinar as forças nos membros BC, BD e CD analisando as juntas B, C e D
Como este é um problema no espaço, analisando as juntas podemos determinar até três forças, pois podemos escrever três equações de equilíbrio e analisando as juntas podemos observe que existem quatro forças desconhecidas agindo. Ao determinar as forças de reação do diagrama de corpo livre, haverá três incógnitas atuando em cada junta.
Passo 2
Observe que, como o triângulo △ BCD é a distância equilateral entre o ponto D e o eixo y é igual à altura do triângulo
Uma vez que a distância entre o ponto A e o eixo y é
Ao analisar a soma dos momentos sobre o eixo y, podemos determinar a força de reação ND
Ao analisar a soma dos momentos sobre o eixo x, podemos determinar a força de reação NC
Finalmente, ao igualar a soma das forças na direção textitz a zero, podemos determinar a força de reação ND
Passo 3
Ao analisar a junta B, podemos agora determinar as forças nos membros AB, BC e BD
Vamos supor que todos os membros estejam em tensão
Podemos notar que o membro BC é paralelo ao eixo y, portanto, podemos escrever força BC como
Também podemos notar que a força de reação NB é paralela ao eixo z, portanto, podemos escrever a força NB como
Podemos escrever o vetor força AB como um produto de sua magnitude AB e um vetor unitário da direção da força (uma vez que assumimos que o membro AB está na tensão, a direção da força vai do ponto B em direção a A)
´Podemos ver na figura que as coordenadas do ponto B e A são
A
Uma vez que conhecemos dois pontos da linha de ação, escrevemos como
Passo 4
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações do equilíbrio
(1)
(2)
(3)
Da equação (3) determinamos a força no membro AB
Da equação (1) determinamos a força do membro BD
Da equação (2) determinamos a força do membro BC
Passo 5
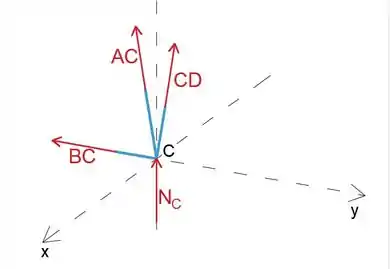
Ao analisar a junta C, podemos agora determinar a força no membro CD
Podemos notar que a força de reação NC é paralela ao eixo z, portanto, podemos escrever a força NC como
Podemos escrever o vetor de força CD como um produto de sua magnitude CD e um vetor unitário de direção de força
Podemos observar da figura que as coordenadas do ponto C e D
Uma vez que conhecemos as duas linhas de ação, podemos escrever como
Passo 6
Podemos escrever o vetor de força CA como um produto de sua magnitude CA e um vetor unitário de direção de força
Podemos ver da figura que as coordenadas dos pontos C e A são
Uma vez que conhecemos dois pontos na linha de ação, escrevemos como
Passo 7
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações do equilíbrio
(4)
(5)
(6)
Da equação (6), podemos determinar a força no membro AC
Por fim, da equação (4), podemos determinar a força no membro CD