Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 87
No grampo de mola mostrado, uma mola interna é enrolada em torno do pino em e as extremidades da mola se apoiam nas superfícies internas das metades do cabo para fornecer a força de aperto desejada. Na posição mostrada, uma força de magnitude é necessária para liberar a braçadeira. Determine a força compressiva em se .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força compressiva em quando , sabendo que, para a posição mostrada, é necessário .
Então bora resolver! Esse problema é bem simples, vamos começar analisando o diagrama de corpo livre, especialmente da parte superior da estrutura. Uma vez que ela é simétrica, o que for feito para a parte de cima vale para a de baixo.
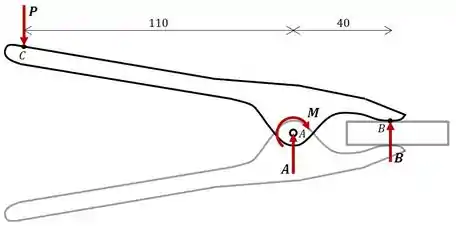
Ou seja, estamos trabalhando com o membro , onde é o ponto de aplicação da força na parte superior da estrutura.
A mola interna enrolada em torno do pino está caracterizada como o momento que essa mola produz.
Passo 2
Show! Agora vamos analisar os dados que nós temos. Na nossa condição inicial, para a força aplicada em , a reação em é igual a zero. Como a estrutura deve estar em equilíbrio, podemos usar o somatório de momentos em torno de para encontrar o momento produzido pela mola.
Passo 3
Tranquilinho né? Agora que temos o momento da mola, podemos analisar quando para encontrar a reação . Pela mesma condição de equilíbrio da estrutura, vamos repetir o somatório de momentos em torno de para obter :
É só isso, galera! Bem de boa né?!
Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 