Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 47
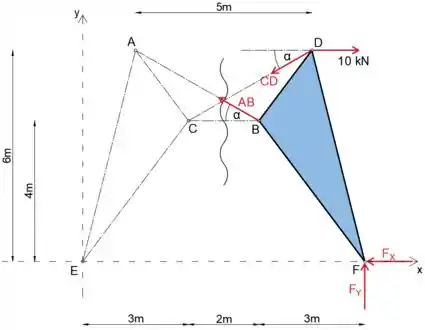
Os quadros articulados ACE e DFB são conectados por duas barras articuladas, AB e CD, que se cruzam sem serem conectadas. Calcule a força em AB.
Passo 1
Aqui temos quatro forças de reação, portanto não podemos determinar aquelas do diagrama de corpo livre, também temos mais de duas incógnitas agindo em cada junta e não podemos isolar uma parte de uma treliça com menos de quatro forças desconhecidas.
Passo 2
Mas se passarmos uma seção pelos membros AB e CD e analisarmos a parte da treliça à esquerda e à direita, teremos seis forças desconhecidas e seis equações.
No final, ao igualar a soma dos momentos sobre o ponto E a zero da parte esquerda e a soma dos momentos sobre o ponto F a zero da parte direita do truste, obteremos 2 equações com 2 incógnitas
Passo 3
Podemos ver que as coordenadas dos pontos A, B e C são
Distância entre A e B na direção x é
Distância entre A e B na direção y é
Portanto, o ângulo que o membro AB machos com eixo X é
Uma vez que a estrutura é simétrica, o membro CD fará o mesmo ângulo com o eixo x que o membro AB
Passo 4
Primeiro, vamos analisar a parte da treliça à esquerda
Vamos supor que todos os membros estão em tensão
Podemos expressar a força AB em função de CD
Passo 5
Agora podemos analisar a parte da treliça à direita
Podemos substituir AB pela expressão (1)
Passo 6
Finalmente, colocando o valor de CD na expressão (1), podemos determinar a força no membro AB
Passo 7
Como obtivemos resultado negativo, isso significa que o membro AB está em compressão
