Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 5

O bloco de 1,5 kg desliza ao longo de um plano liso e bate em uma mola não linear com uma velocidade de v = 4   m / s . A mola é denominada ‘não linear’ porque ela tem uma resistência de F s = k s 2 onde k = 900   N / m 2 . Determine a velocidade do bloco após ele ter comprimido a mola de s = 0,2   m .

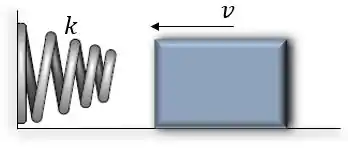
Passo 1

O enunciado nos deu as seguintes informações:

Massa do bloco: m = 1,5   k g ;

Velocidade de encontro com a mola: v = 4   m / s ;

Constante elástica da mola: k = 900   N / m 2 ;

Resistência da mola: F s = k s 2 ;

Espaço comprimido da mola: s = 0,2   m .

Devemos determinar a velocidade do bloco após comprimir a mola.

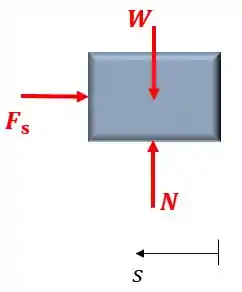
Aqui, podemos pensar como dois momentos. No momento (1), no instante que o bloco toca na mola, temos que

s 1 = 0

v 1 = 4

No momento (2), no instante em que o bloco comprime a mola em0,2 metros, temos que

s 2 = 2   m

v 2 = v

Passo 2

Na direção do deslocamento, somente a força de resistência da mola está em ação, porém em sentido oposto ao deslocamento. Logo, possuirá valor negativo.

Agora vamos aplicar o Princípio do Trabalho e da Energia.

T 1 + ∑ U 1 - 2 = T 2

Onde

T 1 = 1 2 m v 1 2 = 1 2 1,5 4 2 = 12

T 2 = 1 2 1,5 v 2 = 0,75 v 2

∑ U 1 - 2 = - ∫ 0 0,2 k s 2 d s = - ∫ 0 0,2 900 s 2 d s

Substituindo esses valores na equação principal, obtemos

12 - ∫ 0 0,2 900 s 2 d s = 0,75 v 2

12 - 3 00 s 3 0 0,2 = 0,75 v 2

12 - 300 0,2 3 = 0,75 v 2

v = 3,58   m / s

Resposta

v = 3,58   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cursor A de 15k g é liberado a partir do repouso na posição mostrada e desliza com atrito desprezível para cima na haste fixa inclinada de 30 ° em relação à horizontal sob a ação de uma força consta
O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros, e parte do topo da estrutura A com uma velocidade Va = 3 m/s. Determine a altura mínima h da estrutura de maneira que o ca
O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros. Se ele é solto do repouso no topo da estrutura A, determine a altura mínima h da estrutura de maneira que o carrinho dê a
O anel de 2,5 kg é solto do repouso em A e desloca-se ao longo da guia sem atrito. Determine a velocidade do anel quando ele bate no apoio B. A mola tem um comprimento não deformado de 0,15m.
O anel de 2kg é submetido a uma velocidade para baixo de 4m/s quando está em A. Se a mola tem um comprimento não deformado de 1m e uma rigidez k=30N/m, determina a velocidade do anel em s=1m