Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 97

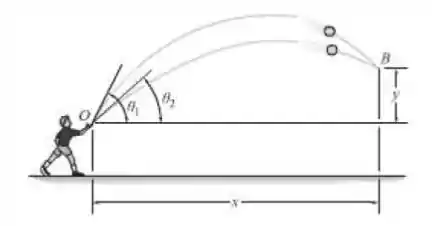
Um garoto joga no ar uma bola a partir de O com uma velocidade v 0 em um ângulo θ 1 . Se ele em seguida joga outra bola com a mesma velocidade v 0 a um ângulo θ 2 < θ 1 , determine o tempo entre os lançamentos de maneira que as bolas colidam em pleno ar em B.

Passo 1

A chave deste problema está em escrevermos as componentes x e y das velocidades de cada uma das bolas e as relações de semelhança entre ambas as bolas. Mas antes disto, vamos tentar entender o problema. Ambas as bolas estão sujeitas a ação da gravidade no eixo y . Este é o motivo dela fazer um arco, subindo e depois descendo.

Agora, decompondo as velocidades de ambas, temos:

v 1 x = v 0 ⋅ cos ⁡ θ 1

v 1 y = v 0 ⋅ sen ⁡ θ 1

v 2 x = v 0 ⋅ cos ⁡ θ 2

v 2 y = v 0 ⋅ sen ⁡ θ 2

Como a bola 1 possui um ângulo de inclinação maior que a bola 2, ela terá uma maior velocidade no eixo y (o que fará com que ela suba mais), e menor velocidade em x . Esta é a razão de ambas se encontrarem em um ponto depois!

Passo 2

Vamos escrever relações entre as bolas. Começaremos pela análise da posição de ambas no eixo y . Assumindo que ambas partem da origem do sistema ( s 0 = 0 ) , a partir das equações da cinemática, teremos para a bola 1:

s = s 0 + v y t 1 + a t 1 2 2

y = 0 + v 0 ⋅ sen ⁡ θ 1 ⋅ t 1 - g t 1 2 2

Já para a bola 2, teremos:

s = s 0 + v y t 2 + a t 2 2 2

y = 0 + v 0 ⋅ sen ⁡ θ 2 ⋅ t 2 - g t 2 2 2

Igualando ambas as equações da bola 1 e 2, temos:

v 0 ⋅ sen ⁡ θ 1 ⋅ t 1 - g t 1 2 2 = v 0 ⋅ sen ⁡ θ 2 ⋅ t 2 - g t 2 2 2

v 0 ⋅ sen ⁡ θ 1 ⋅ t 1 - v 0 ⋅ sen ⁡ θ 2 ⋅ t 2 = g 2 ⋅ t 1 2 - t 2 2

Passo 3

Vamos fazer o mesmo procedimento, só que para o eixo x . Para a bola 1, temos:

s = s 0 + v x t 1

x = 0 + v 0 ⋅ cos ⁡ θ 1 t 1

Já para a bola 2, temos:

s = s 0 + v x t 2

x = 0 + v 0 ⋅ cos ⁡ θ 2 t 2

Igualando ambas as equações, obtemos:

v 0 ⋅ cos ⁡ θ 1 t 1 = v 0 ⋅ cos ⁡ θ 2 t 2

t 2 = cos ⁡ θ 1 cos ⁡ θ 2 ⋅ t 1

Passo 4

Agora que conseguimos determinar uma relação entre os tempos t 1 e t 2 , vamos substituir esta relação na outra equação descoberta no Passo 2. Desta forma,

v 0 ⋅ sen ⁡ θ 1 ⋅ t 1 - v 0 sen ⁡ θ 2 cos ⁡ θ 1 cos ⁡ θ 2 t 1 = g 2 ⋅ t 1 2 - cos 2 ⁡ θ 1 cos 2 ⁡ θ 2 ⋅ t 1 2

Resolvendo esta equação, obtemos:

t 1 = 2 v 0 cos ⁡ θ 2 ( cos ⁡ θ 2 sen ⁡ θ 1 - sen ⁡ θ 2 cos ⁡ θ 1 ) g cos 2 ⁡ θ 2 - cos 2 ⁡ θ 1

t 1 = 2 v 0 cos ⁡ θ 2 sen ⁡ ( θ 1 - θ 2 ) g cos 2 ⁡ θ 2 - cos 2 ⁡ θ 1

Já para o tempo t 2 , temos:

t 2 = 2 v 0 cos ⁡ θ 1 sen ⁡ ( θ 1 - θ 2 ) g cos 2 ⁡ θ 2 - cos 2 ⁡ θ 1

Portanto a diferença dos tempos Δ t é:

Δ t = t 1 - t 2 = 2 v 0 sen ⁡ ( θ 1 - θ 2 ) ⋅ ( cos ⁡ θ 2 - cos ⁡ θ 1 ) g cos 2 ⁡ θ 2 - cos 2 ⁡ θ 1

Δ t = 2 v 0 sen ⁡ ( θ 1 - θ 2 ) g cos ⁡ θ 2 + cos ⁡ θ 1

Resposta

Δ t = 2 v 0 sen ⁡ ( θ 1 - θ 2 ) g cos ⁡ θ 2 + cos ⁡ θ 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para atender a critérios de projeto, pequenas esferas de rolamento devem saltar através de uma abertura de tamanho limitado no topo de sua trajetória após repercutir a partir de uma chapa inerte como
Um jogador de ferradura lança a ferradura em A com uma velocidade inicial v 0 = 11m / s . Determine a faixa para o ângulo de lançamento θ para o qual a ferradura baterá na estaca vertical de 350m m .
Um menino lança uma bola para cima com uma velocidade v 0 = 12m / s . O vento transmite uma aceleração horizontal de 0,4m / s 2 para a esquerda. Em que ângulo θ a bola deve ser atirada para que esta r
O jogador de basquete gosta de arremessar seu lance livre em um ângulo θ = 50 ° com a horizontal como mostrado. Que velocidade inicial v 0 fará com que a bola passe através do centro do aro?
A velocidade de disparo de um fuzil de longo alcance em A é u = 400m / s . Determine os dois ângulos de elevação θ , que permitirão ao projétil acertar a montanha no alvo B .