Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 5

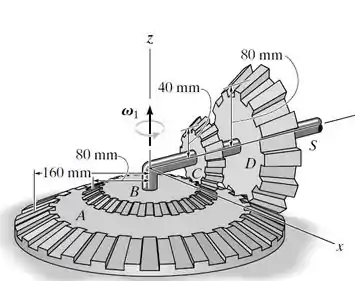
As engrenagens A e B estão fixas, enquanto as engrenagens C e D estão livres para girar em torno do eixo S. Se o eixo gira em torno do eixo z com uma taxa constante de w 1 = 4   r a d / s , determine a velocidade angular e a aceleração angular da engrenagem C.

Passo 1

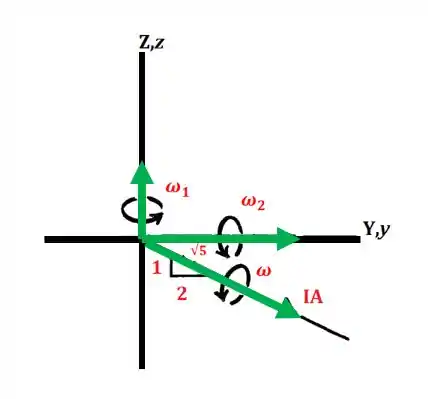
A velocidade angular resultante ω = ω 1 + ω 2 é sempre direcionada ao longo do eixo instantâneo de velocidade zero IA.

ω = ω 1 + ω 2

2 5 ω j - 1 5 ω k = 4 k + ω 2 j

Equacionando as componentes j e k:

- 1 5 ω = 4 2 5 ω = ω 2

Solucionando o sistema temos que :

ω =   - 8,944   r a d / s

ω 2 =   - 8   r a d / s

Assim :

ω = 2 5 - 8,944 j   - 1 5 - 8,944 k = - 8 j   + 4 k   r a d / s

Passo 2

A aceleração angular será:

α = ω = ˙ ( ω ˙ 1 ) X Y Z + ( ω ˙ 2 ) X Y Z (1)

Para ω 2 , Ω = ω 1 = 4 k   r a d / s

( ω ˙ 2 ) X Y Z = ω ˙ 2 x y z + Ω × ω 2

( ω ˙ 2 ) X Y Z = 0 + ( 4 k ) × ( - 8 j )

( ω ˙ 2 ) X Y Z = 32 i   r a d / s 2 (2)

Para ω 1 , Ω = 0

( ω ˙ 1 ) X Y Z = ω ˙ 1 x y z + Ω × ω 1 = 0 + 0 × 0 (3)

Passo 3

Substituindo (2) e (3) em (1), a aceleração angular será:

α = 0 + 32 i = 32 i   r a d / s 2

Resposta

De acordo com os passos 1,2 e 3 a velocidade angular e a aceleração angular da engrenagem C serão respectivamente:

ω = 2 5 - 8,944 j   - 1 5 - 8,944 k = - 8 j   + 4 k   r a d / s

α = 0 + 32 i = 32 i   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco gira em torno de um eixo fixo através de O com velocidade angular ω = 5 r a d / s e aceleração angular de α = 3r a d / s 2 no instante representado, nos sentidos indicados. O cursor A se deslo
O cursor A oscila na ranhura em torno da posição neutra O com uma frequência de dois ciclos por segundo e uma amplitude x m a x = 50 m m de modo que o seu deslocamento em milímetros pode ser escrito x
Se os carros do prob. 5/171 têm ambos uma velocidade constante de 72 km/h enquanto contornam as curvas, determine a aceleração que A parece ter para um observador se deslocando e girando com o carro B
O transporte aéreo B está voando com uma velocidade constante de 800 km/h em um arco horizontal com 15 km de raio. Quando B atinge a posição mostrada, a aeronave A, voando para sudoeste a uma velocida
Uma pista de boliche lisa é orientada na direção norte-sul como mostrado. Uma bola A é liberada com uma velocidade v ao longo da pista conforme indicado. Em função do efeito de Coriolis, a bola desvia