Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 110
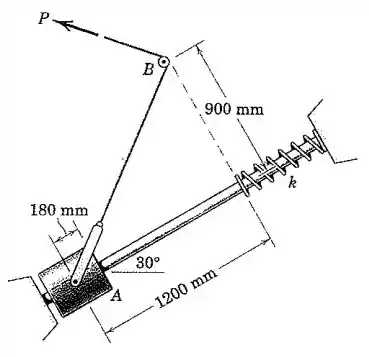
O cursor de é liberado a partir do repouso na posição mostrada e desliza com atrito desprezível para cima na haste fixa inclinada de em relação à horizontal sob a ação de uma força constante aplicada ao cabo. Calcule a rigidez necessária da mola de modo que a sua deflexão máxima seja igual a . A posição da pequena polia em é fixa.
Passo 1
Primeiramente, vamos tentar determinar o trabalho realizado pela força . Perceba que a direção pela qual essa força age no cursor está sempre na reta que vai do cursor até a polia . Então, essa direção está sempre mudando.
Um modo de calcular o “deslocamento” na direção dessa força seria subtrair as distâncias inicial e final de até , ou seja, o deslocamento seria:
E então o trabalho dessa força é dado assim:
Passo 2
Além da força , o peso e a força elástica também realizam trabalho sobre o cursor. Vamos calcular cada um deles:
Passo 3
O cursor foi liberado do repouso, e na deflexão máxima, a velocidade volta a ser zero. Logo, consideraremos que a variação de energia cinética é nula. Então, lembrando que o trabalho total realizado sobre o cursor é igual à sua variação de energia cinética, temos: